Why are the most complex equations of physics so difficult?

The Navier-Stokes equations describe simple everyday phenomena, such as water flowing from a garden hose - but they are based on a task, the solution of which was estimated at a million dollars.

In physics, there are equations that describe everything, from the stretching of space-time to the flight of a photon. However, only one set of equations is considered so mathematically complex that it was chosen as one of the seven Millennium Problems , for which the Clay Mathematical Institute offers a million dollar prize: these are the Navier-Stokes equations describing the flow of fluids.

Recently, I wrote about how a new important result was obtained for these equations. And this work shows that progress towards the Millennium Prize will be more difficult than expected. Why are these equations describing such familiar phenomena as water flowing through a hose mathematically much more difficult to understand than, say, Einstein's field equations that include such stunning objects as black holes?

The answer, as I understand it, lies in turbulence. We all experienced this phenomenon while flying in non-uniform air at an altitude of 10,000 m, or while observing a funnel from the bath water flowing into the sink. However, knowledge does not follow knowledge: turbulence is one of the least understood areas of the physical world.



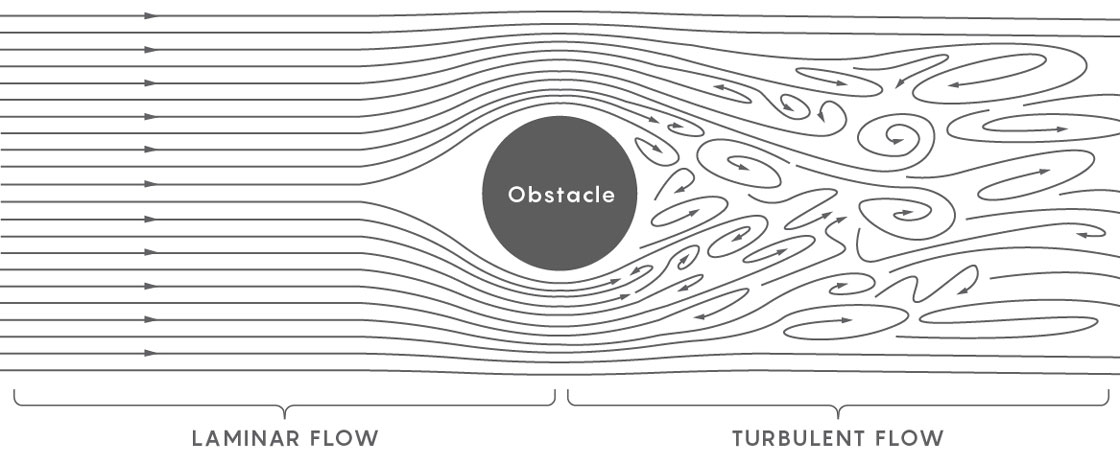
An example of a flow without turbulence is a calm river. Each part of it moves in the same direction at the same speed. Turbulent fluid appears when the flow of a river breaks down so that different parts of the flow begin to move in different directions at different speeds. Physicists first describe the formation of turbulence as the appearance of a funnel in a smooth flow, and then as the formation of small funnels in the first funnel, and even smaller funnels in these funnels - a sea of ​​funnels going into the liquid, so that the liquid is divided into discrete parts, each of which interacts with each other and moves in its own direction.

Researchers want to understand exactly how a smooth flow breaks into turbulent turbulence, and to model the future shape of a fluid, after the turbulence has taken its toll. But the Millennium Problem is formulated more modestly: it is only necessary to prove that solutions always exist. That is, the question is, can equations describe any fluid, with any initial conditions, and to an infinitely distant future?

“The first step is to just try to prove that the equations have some solutions,” says Charlie Fefferman, a mathematician at Princeton University. “It does not give a real understanding of the behavior of liquids, but if you don’t have it, you don’t know anything at all.”

So how can you prove the existence of solutions? You need to start with, in order to understand, because of what they may not be. The Navier-Stokes equations imply the calculation of changes in such quantities as velocity and pressure. Mathematicians are concerned about the following scenario: you run these equations, and after some finite time they tell you that a particle of fluid moves at infinite speed. And this is a problem - to calculate the change in the infinite value is not easier than to divide by zero. Mathematicians call such situations an “explosion”, and in the case of an explosion, the equations stop working and no solutions are found.


The Navier-Stokes equations describe the flow of incompressible fluid.

In general, the product of mass (blue part) and acceleration (violet) is equal to the forces acting on the liquid (orange):

• ρ is the fluid density;
• dV / dt - change in speed over time;
• V ∇V - speed and direction of motion;
• ∇P - change in internal pressure;
• ρ g - the influence of external forces (for example, gravity);
• μ ∇ ² V is the effect of internal forces (viscosity).

Proving the absence of explosions (and the existence of solutions) is tantamount to proving that the maximum velocity of any fluid particle remains limited to some finite value. One of the most important quantities is the kinetic energy of the fluid.

When you start to simulate flow using the Navier-Stokes equations, your fluid has some initial amount of energy. In turbulent flows, energy may begin to concentrate. Instead of spreading evenly throughout the river, the kinetic energy can be collected in whirlpools of arbitrarily small size, and the particles in these whirlpools (theoretically) can accelerate to infinite speed.

“When moving to a smaller and smaller scale, the kinetic energy becomes less and less useful for controlling the solution. A decision can do anything, and I won’t know how to control it, ”says Vlad Vikol, a mathematician at Princeton University who wrote a new job with Tristan Backmaster.

Mathematicians classify partially differential equations on the basis of the extent to which they can begin to behave badly on infinitely small scales. The Navier-Stokes equations are at the extreme end of this scale. The complexity of the mathematics of equations in a sense reflects the complexity of turbulent flows, which they should be able to describe.

“When you zoom in on a place, then from a mathematical point of view, you lose information about the solution,” says Vikol. “But turbulence should describe just that — the transfer of kinetic energy from large to smaller and smaller scales, so she really asks you to increase the scale.”



Speaking about the mathematical properties of physical equations, it is natural to ask the question: will this reasoning change how we regard the physical world? In the case of the Navier – Stokes equations and the Millennium Problem, the answer will be both “yes” and “no”. After almost 200 years of experiments, it is clear that the equations work: the flow predicted by Navier-Stokes consistently coincides with the flow observed in the experiments. If you are a physicist working in a laboratory, this may be enough for you. But mathematicians need to know more - they want to check whether these equations can be followed all the way, to follow exactly how the flow changes, from one point of time to another (for any initial fluid configuration), and even to catch the source of turbulence.

“The behavior of liquids is fraught with surprises,” says Fefferman. “These surprises are basically explained by the fundamental equations that control the flow of liquids, but how to move from the equations that control the movement of a liquid to the description of how the liquid actually moves is a mystery.”