Polynomials and Splines Programmer's Guide

So you are a programmer. Why do you need polynomials at all? For example, because it is a good geometric clay, from which you can make different things.

From our article explaining the essence of mathematical analysis on the example of python, blood and dynamite, it is clear that you can analyze and synthesize arbitrary functions as polynomials. However, it is not necessary to work with functions. Sometimes you may need to simulate a spline from several points or properties, like tangent curves. For example, you need to make some kind of animation, or a nice video effect, or draw a curve through certain points, or create a flat surface in one place and curved in another.

Polynomials, including even splines, may not always be the best tool for this task, but they have some features that programmers appreciate. They are simple and versatile in nature, and also, most importantly, very effective in terms of performance. Take for example the following polynomial:



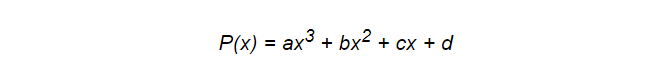
To calculate it, only 6 multiplication actions and 3 additions are required. This is important because your model will be constantly subjected to calculations. But here we can make optimization. This will help us Horner's scheme. With its help, the same polynomial can be written as



And this is only 3 multiplications and 3 additions. You see, we just started, and you have already learned how to get rid of one third of the calculations.

Polynomial interpolation

The task of adapting a polynomial of the nth degree under n + 1 point of space is called polynomial interpolation. There are several ways to implement it. You can use the Newton or Lagrange interpolation formulas, but the easiest way to obtain an interpolation polynomial is to solve a system of linear equations.

If a polynomial passes through a point, then we obviously can assert that P (xi) = yi . Suppose we want to adapt a polynomial to a set of three points. It means that:



In general, we cannot draw a line through three arbitrary points. And therefore we have to twist it, forming a parabola. Or, in other words, introduce a second degree polynomial, also known as a quadratic function.



Since xs and ys are known, we can only solve the system and find out the coefficients a, b, c, and since this system consists of three equations and three variables, we can usually get a single solution.

To see this, try moving the position of the three points on the lower graph and see what happens.



This graph is also very useful for the mental analysis of linear systems. In the general case, it is impossible to fit a straight line at three points, just as it is impossible to find a solution for a system of n equations with n-1 unknown variables. But sometimes it is possible. For example, in cases when some of the points coincide or all of them are intentionally located on one straight line.

The reverse situation is even more interesting. We can draw an infinite number of parabolas through two given points. All of them are equally suitable as a solution to the problem. And at the same time, we cannot get some uniquely better solution for systems of n equations and n + 1 variables.

But what if it's still possible? What if we can introduce some additional criteria for choosing the most appropriate option?

Synthesis

Similar questions lead us to the territory of polynomial synthesis. In our case, this is a cross between polynomial series and polynomial interpolation. With the help of series, we can model a function based on its derivatives at some point, and with the help of synthesis, we can use both points and derivatives (and not only them, but about this another time).

The derivative of a function is closely related to the geometric properties of its graph. The first derivative determines the tangent of the slope of the tangent, and the second - the curvature.

Suppose we need to define a function passing through two points, knowing its tangent at both points. In this case, we can easily synthesize it in the form of a polynomial.

As before, we need to write down the system of equations. Now we need four conditions, so we should choose a polynomial of degree 3, that is, a cubic function.



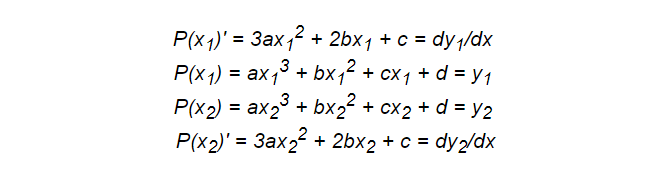
Some of the equations are based on points, and others are derived. Here you can also add integrals for the introduction of the necessary properties of integerness, which makes this technique quite effective.

But we will continue to consider a function connecting two points of a continuous smooth line with tangential constraints at these points.

Runge Phenomenon

Polynomial interpolation has an unpleasant property, manifested in an increase in the growth of oscillations at both ends of the interval with an increase in the number of points. This phenomenon is called the Runge phenomenon. It limits the use of simple polynomial interpolations.

Another disadvantage of this approach is its globality, that is, the change of the entire function together with the slightest change in the position of at least one point. In combination with oscillations, it turns out the most chaos.

Chebyshev nodes

One of the ways to combat chaos is to select a special mesh for interpolation - Chebyshev nodes . These are special values ​​of x, which are obtained by dividing a semicircle with radius 1 into equal fragments and projecting them onto the x axis.

In general, in this technique lies a certain mathematical magic, but from a pragmatic point of view, it is intended to minimize the phenomenon of Runge. And although it does not allow to make the interpolation completely predictable, everything works stably on the segment (-1: 1).



Of course, you can extend the interval along the X axis as much as you need using a one-dimensional affine transform. It is not necessary to stick to the segment (-1; 1) .

But interpolation at the same time retains its ubiquity. Changing the first point still affects the function of the function near the last, although not so significantly.

Splines

There are quite a few varieties of splines, but they all share one application scenario. As soon as the global interpolation for any reason ceases to be suitable for our tasks, we can divide our interval into smaller fragments and define separate functions for interpolation on each of them.

The only thing we need to consider is the need to connect them at the ends to maintain continuity. If we guarantee the continuity of not only the final, piecewise-given function, but also its first derivative, then the tangents of each of its segments will coincide, and its graph will look smooth.

There is a certain classification of splines. For example, take a polynomial spline consisting of two fragments. If each of its fragments is determined by a polynomial of third degree, then it is called cubic. It may have, for example, such a property as the continuity of the first derivative, since the tangents at the junction of the fragments coincide. Its fragments are not equal to the width. It is not of natural origin, as we can manage the derivatives at its ends. And of course, this is an interpolation spline, since it passes exactly through the grid points we have indicated.

Conclusion

The likelihood that you will ever have to implement in practice your own interpolation is extremely small. There are many ready-made solutions and in most cases you will just have to choose the right tool for the job. This area of ​​knowledge is not so difficult, but the number of unknown words and names may repel.

The goal of this guide was to provide you with a basic understanding of the ideas used to work with polynomials and splines. In no case does he claim to be complete, because in fact, entire books have been written for each of the small chapters of this material. But we hope, at least, that an interactive approach to the presentation in this material will be useful not only for a brief introduction, but if such a need arises, it will help you to master more advanced topics.