Mathematical Chaos Models

Introduction

Habr has already discussed chaos theory in [1,2,3]. In these articles, the following aspects of chaos theory are considered: a generalized scheme of the Chua generator; modeling the dynamics of the Lorentz system; programmable logic integrated circuits attractors of Lorentz, Roessler, Rikitake and Nose-Hoover.

However, the chaos theory techniques are also used to model biological systems, which are undoubtedly one of the most chaotic systems of all that one can imagine. Dynamic equality systems were used to simulate everything — from population growth and epidemics to arrhythmic heartbeats [4].

In fact, almost any chaotic system can be modeled - the stock market generates curves that can be easily analyzed with the help of strange attractors, the process of dropping drops from a flowing water faucet seems random when analyzed with the naked ear, but if depicted as a strange attractor, supernatural order, which could not be expected from traditional means.

The purpose of this article is to examine the theory of chaos on the example of increasing the number of biological populations and doubling the cycle in mechanical systems with graphical visualization of mathematical models based on simple, intuitive programs written in Python.

The article is written for the purpose of learning, but will allow even the reader who does not have programming experience, using the above programs, to independently solve most of the new training tasks on the topic of modeling chaos.

Doubling the period of cycles and chaos on the example of the growth of the number of biological populations

We begin by considering a logistic differential equation that models a limited, rather than an exponential increase in the number of biological populations:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

It is this equation that can predict exotic and unexpected patterns of behavior of some populations. Indeed, according to (1) with $$$t \ rightarrow + \ infty$ population size approaches the boundary equal to a / b .

For the numerical solution of the logistic differential solution, you can use the simplest algorithm, with the numerical value of the time step, taking $$$t_ {n + 1} = t_ {n} + h$ , then solution (1) can be obtained by repeatedly applying the following relationship:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ (2)

Represent equation (2) in the form of a logistic equation in finite differences:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

where: r = 1 + ah and s = bh .
Substitution in (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ , we obtain an iterative formula:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ , (four)

By calculating the values ​​given by relation (3), you can generate a sequence $$$x_ {1}, x_ {2}, x_ {3}, .....$
the maximum values ​​of the number of populations that will be maintained by the environment at specified points in time $$$t_ {1}, t_ {2}, t_ {3}.$ .

We assume that there is a limiting value of fractions expressing a part of the population size:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ , (five).

We will explore how it depends $$$x _ {\ infty}$ from the growth parameter r in equation (4). To do this, write a program in Python, which, starting with $$$x_ {1} = 0.5$ , calculates results at several hundred iterations ( n = 200 ) for r = 1.5, 2.0, 2.5 :


The result of the program (to reduce the output of the results are the first three and last four values):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Analysis of the discrete model shows that for r = 1.5, 2.0, and 2.5 with an increase in the number of iterations, the value $$$x_ {n}$ stabilizes and becomes almost equal to the limit $$$x _ {\ infty}$ , which is determined by the relation (5). And for the given values ​​of r value $$$x _ {\ infty}$ respectively equal to $$$x _ {\ infty} = 0.3333; 0.5000; 0.6000$ .
Increase r = 3.1, 3.25, 3.5 and the number of iterations n = 1008, for this we make the following changes to the program:


The result of the program (to reduce the output of the results are the first four and last eight values):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

As follows from the above data, instead of stabilizing near the single limiting population size, the fractional part of the population size fluctuates between two fractions as time changes. Compared to r = 3.1 , the cycle period for r = 3.25 is doubled, and for r = 3.5 it is four times as long.


The result of the program:



Thanks to the doubling period, the iteration, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ became widely known. When the growth rate exceeds r = 3.56 , doubling of the period is accelerated and extreme chaos occurs at the point r = 3.57 . To display the onset of chaos, use the following program:


The result of the program:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

We write a program to visualize the dependence of the behavior of iterations on the growth parameter r . For each value of r in the interval $$$a \ leqslant r \ leqslant b$ 1000 iterations are performed to achieve sustainability. Then, every 250 values ​​obtained as a result of iterations, are plotted on the graph along the vertical axis, forming points ( r, x ):


Result in the form of a diagram:



The resulting graph is called a “branch diagram” , which allows you to determine what this value of r corresponds to - a cycle or chaos. The only value of the population size is determined to $$$r \ approx 3$ then cycle with a period of 2 to $$$r \ approx $ 3.$ , then a cycle with a period of 4, then a cycle with a period of 8 and further with a rapid approach to chaos.

It should be noted that the vertical areas of unfilled space on the graph are the areas r = 3.6 and r = 3.7 , between r = 3.7 and r = 3.8 , between r = 3.8 and r = 3.9 where the cyclic order from the previous chaos returns.
To consider the appearance of a cycle with a period of multiple 3 in $$$3.8 \ leqslant r \ leqslant $ 3.$ make changes to the previous program:


The result of the program:



The cycle of period 3 appears in the vicinity of the point r = 3.83 , and then is broken up into cycles 6,12,24. The existence of a cycle with period 3 implies the presence of cycles of any other finite period, as well as chaotic cycles without a period at all.

The branch diagram allows you to follow the development of the system with a smooth change of the parameter. For a fixed value of the parameter beyond the orbits of the points, a spider diagram can be traced (the Lameray diagram).

Building a spider diagram allows you to identify various effects that are invisible in the branch diagram. Write the program:


Lameray Chart:

Period doubling in mechanical systems

Consider a differential equation that models the free damped oscillations of a material point of a given mass on a nonlinear spring, in which the damping is determined by speed.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

In equation (6), the term kx represents the force of a linear spring applied to the material point of a given mass, and the term $$$\ beta x ^ {3}$ represents the actual nonlinearity of the spring.

If the system of free oscillations (6) is acted upon, then the movement of the material mass point, to which this force is applied, is described by the differential Duffing equation for forced oscillations:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

Equation (7) for the majority of its parameters is solved by a numerical method. The mechanical system for the mathematical model according to equation (7) is shown in the figure:



A feature of the reduced system is that instead of a spring, a flexible metallic thread is used, which oscillates in a vertical plane, for which Hooke’s constant k is negative. In this scheme, the points of stable equilibrium are (a) and (c), and the point of unstable equilibrium is (b).

When the material point is displaced from position (b), the force acting on it is repulsive. If a periodic force, for example, created by an oscillating magnetic field is partially extinguished by air resistance. Then, equation (7) is an acceptable mathematical model for the horizontal displacement x (t) of a material point with the following parameters $$$k <0, c> 0, \ beta> 0$ .

To study the behavior of such a nonlinear system, we take $$$k = -1, m = c = \ beta = \ omega = 1$ , then the differential equation (7) takes the form:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ , (eight)

We write a program for the numerical integration of equation (8) with initial conditions $$$x (0) = 1, x ^ {'} (0) = 0$ in the area of $$$100 \ leqslant t \ leqslant 200$ and for each of the following amplitude values $$$F_ {0} = 0.6; 0.7; 0.75; 0.8$ , and in each case to bring to the graph solutions for planes $$$x (t), x ^ {'} (t)$ and $$$t, x (t)$ :


Graphs as a result of the program





This transition from period doubling to chaos shows the general behavior of a nonlinear mechanical system in response to a change in the corresponding physical parameter, for example: $$$k, m, c, \ beta, \ omega, F_ {0}$ . Such phenomena do not occur in linear mechanical systems.

Lorenz attractor

The substitution in the Duffing equation for forced oscillations (7) leads to a two-dimensional non-linear system of differential equations, as was shown in the previous listing. The three-dimensional nonlinear system of differential equations as applied to meteorology problems was considered by E.N. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

It is better to consider the solution of system (9) in a projection onto one of three planes. Let us write a program for numerical integration with the values ​​of the parameters b = \ frac {8} {3}, s = 10, r = 28 and the initial conditions x (0) = - 8, y (0) = 8, z (0) = 27 :


The result of the program:



Considering the image on the graph in time, it can be assumed that the point P (x (t), y (t), z (t)) performs a random number of oscillations from the right, then from the left. For the meteorological application of the Lorenz system, after a random number of clear days, a random number of rainy days follows.

Consider a program to display the Lorenz attractor in the xyz plane for slightly different initial conditions:


The results of the program are shown in the following graphs:





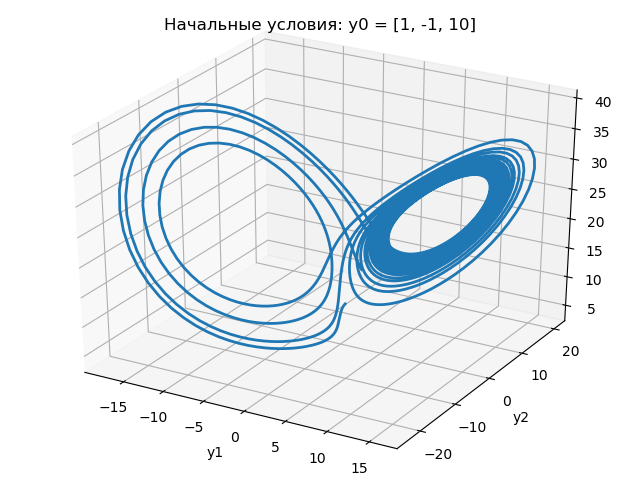
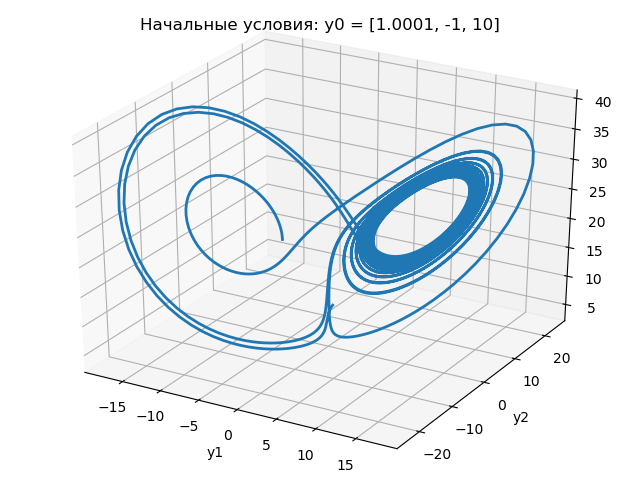
From the above graphs it follows that a change in the initial condition for from 1.0 to 1.0001 dramatically changes the nature of the change in the Lorenz attractor.

Rossler system

This is a very intensively studied nonlinear three-dimensional system:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$ (ten)
$$$\ frac {dz} {dt} = b + x (x-c).$

We write a program for the numerical integration of system (10) for the following parameters a = 0.39, b = 2, c = 4 with initial conditions x (0) = 0, y (0) = 0, z (0) = 0 :


The result of the program:



In the plane, the Rossler ribbon looks like a loop, but in space it turns out to be twisted like a Mobius strip.

findings

To demonstrate the phenomena of chaos are simple and intuitive programs in the high-level programming language Python, which are easy to upgrade to new projects on this topic. The article has an educational and methodical focus and can be used in the learning process.

Links

1. A little bit about chaos and how to create it
2. A critical look at the Lorenz attractor
3. Chaos generators on FPGA
4. Differential equations and boundary value problems: modeling and calculation using Mathematica, Maple and MATLAB. 3rd edition .: Trans. from English - M .: OOO “I.D. Williams ”, 2008. - 1104 pp., Il. - Paral. tit English