Biquaternions

If you opened this article, you probably already heard about quaternions, and maybe even use them in your developments. But it's time to rise to a higher level - to biquaternions.

This article provides basic concepts about biquaternions and operations of working with them. For a better understanding of working with biquaternions, a vivid Javascript example is shown using Canvas.

Biquaternion Definition

A biquaternion is a hypercomplex number with a dimension of 8. In English-language articles and literature, they are called “dual quaternion”; in Russian-language literature there is also the name “dual quaternion” or “complex quaternion”.

The main difference from quaternions is that the quaternion describes the orientation of the object in space, and the biquaternion also the position of the object in space.

Biquaternion can be represented as two quaternions:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - the real part determines the orientation of the object in space;
$$$\ textbf {q} _2$ - the dual part, determines the position of the object in space.

The biquaternion is also called the complex quaternion, in this case it is represented as a quaternion, each component of which is a dual number (not to be confused with the complex). Dual number $$$A = a_1 + \ epsilon a_2$ where $$$a_1$ and $$$a_2$ - real numbers, and $$$\ epsilon$ - the Clifford symbol (complexity) with the property $$$\ epsilon ^ 2 = 0$ . We will not delve into mathematics, since we are more interested in the applied part, so further - we will consider biquaternion as two quaternions.

Geometric interpretation of the biquaternion

By analogy with the quaternion, with which you can set the orientation of the object, you can also set the position by the biquaternion. Those. the biquaternion sets two values ​​at once - the position and orientation of the object in space. If we consider them in dynamics, then the biquaternion determines two quantities — the linear displacement velocity and the angular velocity of rotation of the object. The figure below shows the geometric meaning of the biquaternion.



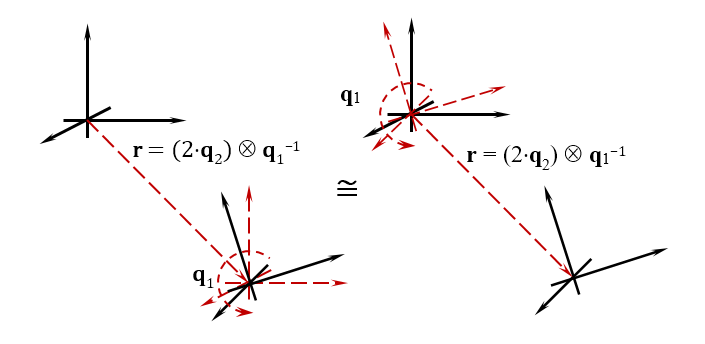
Game developers know that in order to determine the position and orientation of an object in the game space, rotation matrices and displacement matrices are used, and, depending on the sequence in which you use them, the result of the object's final position is different. For those who are accustomed to divide the movement into separate operations, for working with biquaternions, take as a rule: first, move the object, then rotate. In fact, you are describing these two movements with one number, albeit a complex hypercomplex.

Scalar characteristics

Consider the main scalar characteristics. Here it is necessary to pay attention to the fact that they return not ordinary real numbers, but dual ones.

1. The norm of the biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Biquaternion module

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Basic operations

Consider the basic operations of working with biquaternions. As you can see, they are very similar to similar operations with quaternions.

1. Biquaternion conjugation

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Biquaternion addition and subtraction

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

The addition and subtraction of biquaternions is commutative (the terms can be swapped).

3. Multiplication of a real number by a biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Biquaternion multiplication

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

Biquaternion multiplication is noncommutative (when changing the order of factors, the result of biquaternion multiplication is different).

This operation is one of the main ones when working with biquaternions and carries a physical meaning, namely, the result of biquaternion multiplication is the operation of addition of turns and linear displacements of two biquaternions.

5. Reverse biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Determination of biquaternion through orientation angles and position vector

To begin with, we define the coordinate systems in which we will consider the orientation and position of the object in space. This must be done in order to specify the real part of the biquaternion (orientation quaternion), the sequence of turns of which affects the resulting quaternion from the orientation angles. Here we will be guided by aircraft angles - yaw $$$\ psi$ pitch $$$\ vartheta$ and roll $$$\ gamma$ .

We define the basic coordinate system. Imagine that you are standing on the surface of the Earth and look in the direction of the North.

Point O _o - the beginning of the coordinate system, located at the point of the beginning of the movement of the object
The axis O _o Y _g - directed vertically upwards, and opposite to the direction of the vector of gravity.
The axis O _o X _g - is directed towards the North, on the tangent of the local meridian.
The axis O _o Z _g - complements the system to the right and is directed to the right, towards the East.

The second coordinate system is connected. Imagine, for example, a plane or other object.
Point O - the origin of the coordinate system, as a rule, is located at the center of mass of the object.
The axis OY is directed vertically upwards and is perpendicular to the horizontal plane of the object.
The axis OX is directed forward to the front point of the object.
Axis OZ - complements the system to the right.

The position of the object in space is given by the radius vector of the beginning (point O ) of the associated coordinate system relative to the fixed base coordinate system. The orientation of the associated coordinate system relative to the base is determined by three successive turns on:

yaw angle $$$\ psi$ - turn around the axis OY ,
pitch angle $$$\ vartheta$ - turn around the axis OZ ,
roll angle $$$\ gamma$ - turn around the axis OX .

For the initial definition of a biquaternion, it is necessary to specify the real and dual parts of the biquaternion. The orientation and position of the object is set relative to a certain basic coordinate system using orientation angles $$$\ psi, \ vartheta, \ gamma$ and the center of mass position vector $$$r = (r_x, r_y, r_z) ^ T$ .

Real part $$$\ textbf {q} _1$ can be set using the formula:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

Note that if you have a different turn sequence, the expressions will be different too.

Dual part $$$\ textbf {q} _2$ determined by the expression:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Calculation of orientation angles and position vector from biquaternion. Inverse transform

The orientation angles can be calculated from the real part of the biquaternion $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

The position of the object is determined by the expression:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

the result is a vector in quaternion form $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Rotate and move the vector by the biquaternion

One of the remarkable properties of biquaternions is the rotation and displacement of a vector from one coordinate system to another. Let O _o X _g Y _g Z _g be the fixed basic coordinate system, and OXYZ be the associated coordinate system of the object. Then the orientation and position of the object relative to the base coordinate system can be set by the biquaternion $$$\ widetilde {\ textbf {q}}$ . If a vector is specified $$$\ textbf {r}$ in a connected coordinate system, then you can get a vector $$$\ textbf {r} _0$ in the base coordinate system using the formula:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

and back:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

Where $$$\ textbf {r}$ - vector in biquaternion form, $$$\ textbf {r} = (1, 0, 0, 0, 0, r_x, r_y, r_z)$

Biquaternion javascript library

All the above operations of working with biquaternions are implemented in the javascript library, depending on your tasks, it can be implemented in other programming languages. The main functions of working with biquaternions:

Function	Description
DualQuaternion.dq	The body of the biquaternion in the form of an array of 8 numbers
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	A constructor that defines a biquaternion by setting all eight numbers.
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Get biquaternion by specifying the orientation of the object by the Euler angles and the object position vector
DualQuaternion.getEulerVector()	Get Euler angles and position vector from biquaternion
DualQuaternion.getVector()	Get position vector from biquaternion
DualQuaternion.getReal()	Get the real part of the biquaternion (determines the orientation of the object in space)
DualQuaternion.getDual()	Get the dual part of the biquaternion (determines the position of the object in space)
DualQuaternion.norm()	Get the rate of the biquaternion in the form of a dual number
DualQuaternion.mod()	Get the biquaternion module as a dual number
DualQuaternion.conjugate()	Get conjugated biquaternion
DualQuaternion.inverse()	Get reverse biquaternion
DualQuaternion.mul(DQ2)	Biquaternion multiplication
DualQuaternion.toString()	Convert the biquaternion to a line, for example, for output to a debug console

An example of working with biquaternions

For a better understanding of the basics of using biquaternions as an example, consider a small game. Sets a rectangular area - the map. On the map floats the ship on which the rotary cannon is mounted. Here it is necessary to take into account that for the ship the base coordinate system is the coordinate system of the map, and for the instrument the base coordinate system is the ship. All objects are drawn in the coordinate system of the map and here it will be interesting to see how you can go from the coordinate system of the instrument to the coordinate system of the map using the biquaternion multiplication property. The movement of the ship is controlled by the keys W, A, S, D. The direction of the weapon is set by the mouse cursor.



A ship and an instrument are described in two classes: Ship and Gun . In the class constructor of the ship, its form in the form of biquaternion points, the initial orientation and position on the map in the form of biquaternion this.dq_pos .

Biquaternion increments are also given when the ship is controlled. When moving back and forth (W, S keys), only the dual part of the biquaternion will change, while right-left controls (A, D keys) the real and dual part of the biquaternion, which sets the angle of rotation, will change.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); // Форма корабля this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); // Приращения текущей позиции при управлении this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

In the class itself, only one function for rendering Ship.draw() implemented. Note the application of the biquaternion multiplication operation of each point of the ship by the current position and orientation of the ship to the biquaternion.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** * Нарисовать кораблик */ 'draw': function() { // Переместить все точки кораблика с помощью бикватернионного умножения v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); // Непосредственно рисование ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

In the constructor of a tool class, its form is specified in the form of biquaternion points. The gun will be displayed as a line. The initial orientation and position on the ship is given by the biquaternion this.dq_pos . Also set and binding to the ship on which it is installed. The instrument on the ship can only rotate, so the biquaternion increments when controlling the instrument will change only the real part of the biquaternion, which sets the angle of rotation. In this example, the tool is guided with the mouse cursor, so the tool will rotate instantly.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; // Позиция орудия относительно корабля this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); // Форма орудия this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); // Вращение орудия при управлении this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

In the tool class, only one of its drawing functions Ship.draw() also implemented. The tool is displayed as a line, which is defined by two points this.dq_backward and this.dq_forward . To determine the coordinates of the instrument points, the operation of biquaternion multiplication is used.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** * Нарисовать орудие */ 'draw': function() { // Переместить орудие относительно корабля v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); // Непосредственно рисование ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

The handling of the ship and instrument control is implemented through events. For pressing and pressing the ship's control keys, four variables are leftPressed, upPressed, rightPressed, downPressed , which are processed in the main program loop.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); // Обработка нажатия клавиш управления function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } // влево A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } // вверх W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } // вправо D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } // вниз S } // Обработка отжатия клавиш управления function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } // влево A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } // вверх W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } // вправо D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } // вниз S } 

One of the most interesting functions in terms of the use of biquaternion operations is to control the ship's instrument in the direction of the mouse pointer. First, the coordinates of the mouse pointer are defined in the dq_mouse_pos biquaternion. Then, the biquaternion position of the mouse relative to the ship is calculated using biquaternion multiplication. The biquaternion of the ship is taken away from the mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Note: read sequential biquaternion multiplication operations from right to left). Finally, the angle between the tool and mouse vectors is determined. The starting point of gun_1.dq_backward assigned the resulting value.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; // Обрабатывать события только когда курсор мышки находится в игровой области if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { // Бикватернион положения мышки dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); // Бикватернион положения мышки относительно корабля // Направление орудия. От координат мышки отнимается координаты корабля // Последовательность бикватернионного умножения важна // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); // Угол между векторами орудия и мышки q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

In the main body of the program, the objects of the ship and the ship_1 and gun_1 tools ship_1 gun_1 , debug information is output and the control of the ship is processed.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); // Управление корабликом if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

The link to the archive contains the full code of libraries working with quaternions and biquaternions, the program script itself and the index.html file, which can be opened locally in the browser in order to run the example discussed above.

An example of working with biquaternions

Conclusion

You may have a question: why use such a complex mathematical apparatus when you can use standard means for moving and rotating objects? One of the main advantages is that the bi-quaternion form of writing is more computationally efficient, since all operations of working with biquaternions after the expansion of expressions are linear. In this video, Geometric Skinning with Approximate Dual Quaternion Blending shows how much more efficient is the calculation using biquaternions in comparison with other methods.

I mainly took information on the use of biquaternions from English-language sources.
From domestic literature, I can advise two books:

1. Chelnokov Yury Nikolaevich. Quaternion and biquaternion models and solid mechanics methods and their applications. Geometry and kinematics of motion. - monumental theoretical work.
2. Gordeev Vadim Nikolaevich. Quaternions and biquaternions with applications in geometry and mechanics. - written in a more understandable language and shows applications in the tasks of shaping curvilinear spatial structures.