Developing a hexapod from scratch (part 3) - Math

Hello! The development of the hexapod is progressing and finally the basic mathematical part has been tested and is ready for documentation. In order for the project to live to the end and not get dusty on the shelf, you need to see its shifts in a positive direction, even if they are minor. In this article I will talk about the algorithm for solving the inverse problem of kinematics and clearly show it in action. I hope it will be interesting.

Coordinate systems

For a start, it’s worth deciding on the coordinate systems of the robot - there are as many as three:

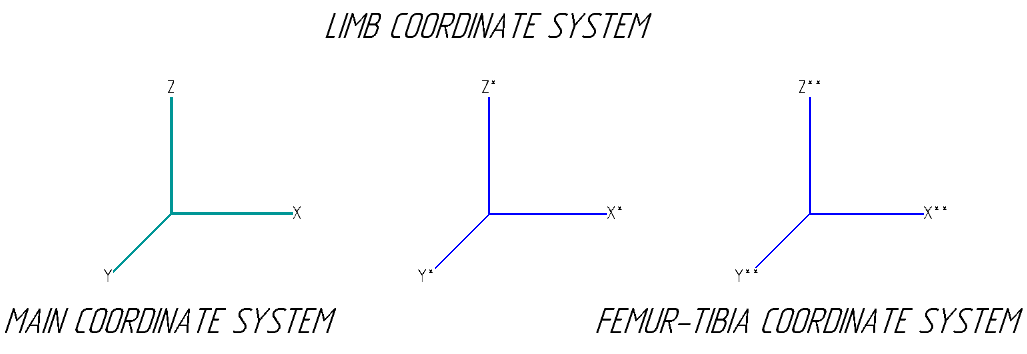
In fact, they are no different from each other, but are located in different parts of the body and can be rotated relative to each other at some angle. When viewed from above, the location of the axes will be as follows (the coxa_zero_rotate parameter will be described a bit later):


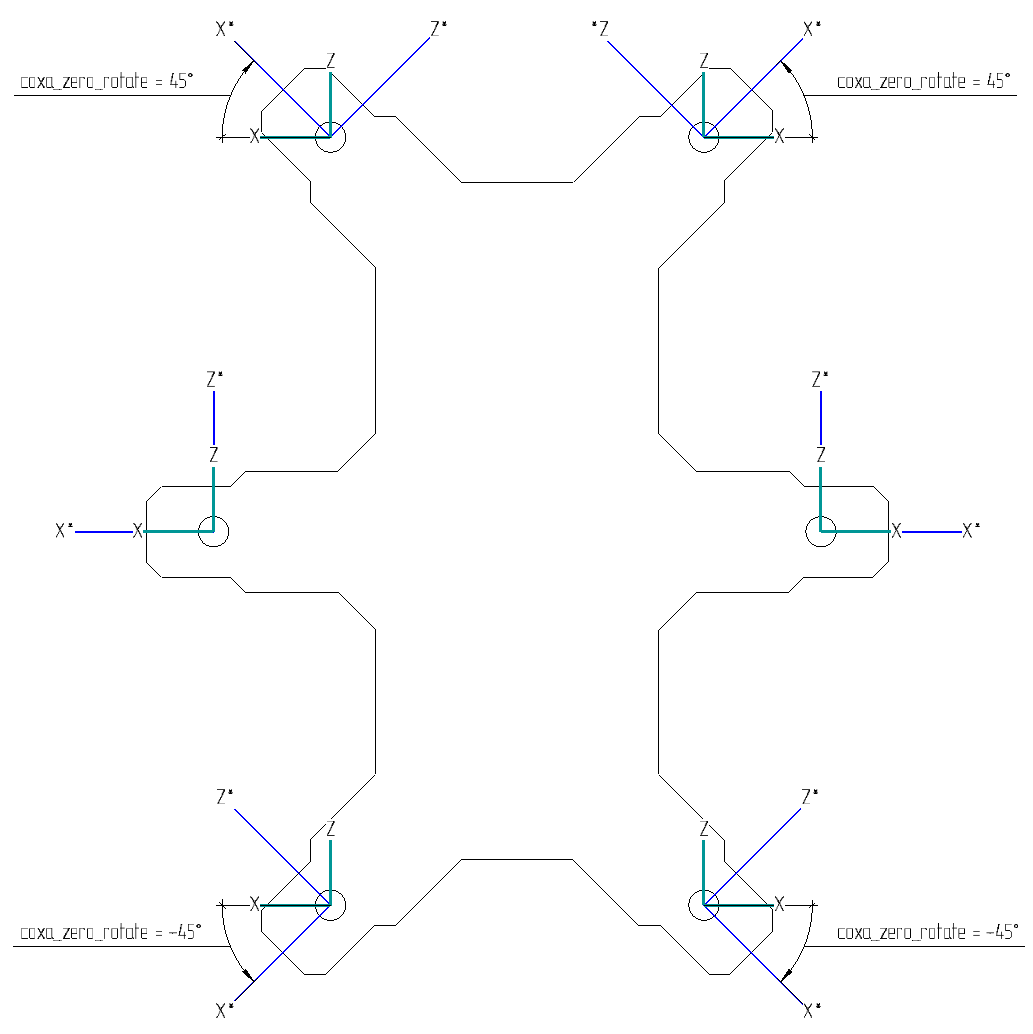
As you may have noticed, the coordinate systems on the left and right sides are located symmetrically relative to the center of the body. It seemed to me that it would be easier.

The coordinates of each point are relative to the limb for which this point is intended. This approach will allow you to safely move the limb anywhere without interfering with the configuration.

And this is how they are located relative to the limb:


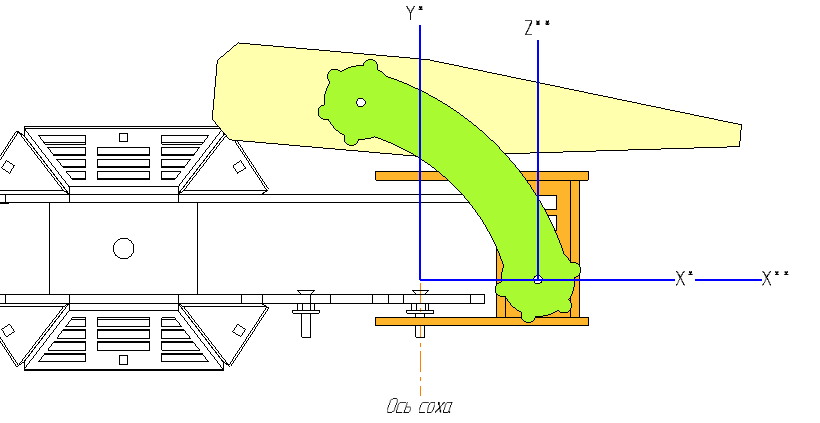
The coordinates of the target point are relative to the MAIN COORDINATE SYSTEM. Initially, I wanted to set the coordinates relative to the center of the case, but this was not very convenient and required storing a number of additional parameters.

Hereinafter, the designation X *, X **, etc. will be replaced by X ′, X ′ ′.

The solution of the inverse problem of kinematics

Let's start with the most difficult and interesting moment for me - kinematics. I invented the algorithm myself, sometimes looking at the properties of the triangle and trigonometric functions. I have a hard time with mechanics, but worse with trigonometry, so maybe I could not take into account something somewhere, but this algorithm works (video at the end).

1. Statement of the problem

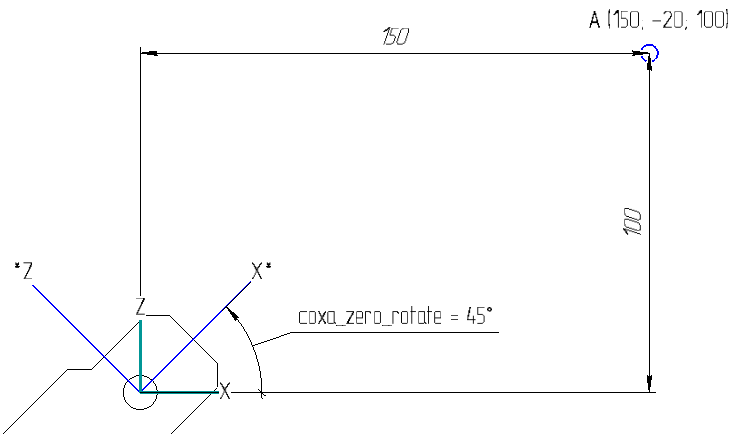
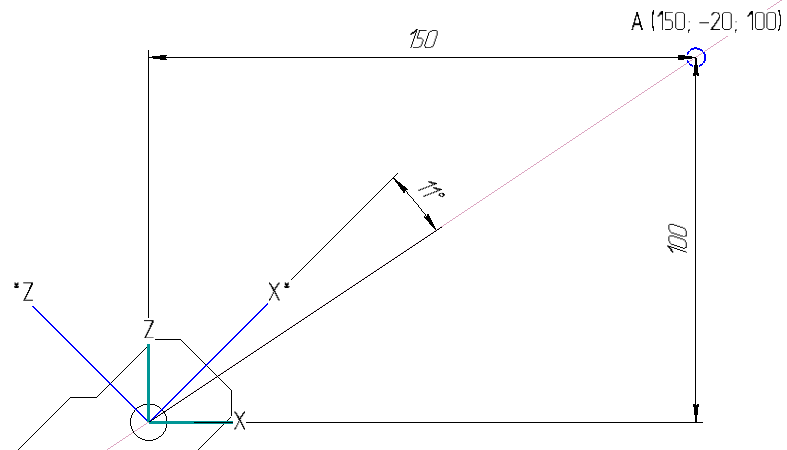
Suppose we need the front right limb to reach point A with coordinates (150; -20; 100). It is also known that the limb is rotated 45 degrees relative to the body (parameter coxa_zero_rotate):


The limb itself has the following parameters:


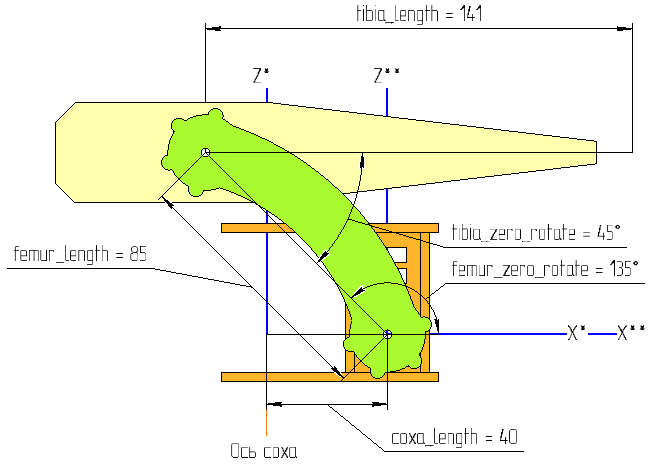
I think it is not necessary to describe what these parameters mean, the names speak for themselves. You can only add that all these parameters are determined by the configuration of the case, are permanent and are stored in FLASH memory with the ability to edit from the outside (for flexibility).


All the above parameters are enough to solve the problem.

2. Problem solving

2.1 Finding the angle of rotation of COXA

This stage is the easiest. First you need to recalculate the coordinates of point A relative to LIMB COORDINATE SYSTEM. Obviously, you need to rotate the angle coxa_zero_rotate, you can do this using the following formulas:

$$$$ display $$ x ′ = x ⋅ cos (α) + z sin (α) = 150 ⋅ cos (45) + 100 sin (45) = 176.78 $$ display $$

$$

$$y ′ = y = -20$$

$$$$ display $$ z ′ = -x ⋅ sin (α) + z cos (α) = -150 sin (45) + 100 ⋅ cos (45) = -35.36 $$ display $$

Thus, we obtained the coordinates of the target point A (176.78; -20; -35.36) relative to LIMB COORDINATE SYSTEM.

Now you can find the angle COXA using the function atan2:

$$

$$COXA = atan2 (z ′, x ′) = atan2 (-35.36, 176.78) = -11.30 °$$

And so, we got the angle to which the COXA servo needs to be turned so that point A is in the X′Y ′ plane. Let's now check our calculations in KOMPAS 3D:


That's right.

2.2 Finding the rotation angle of FEMUR and TIBIA
To find these angles, it is necessary to go to the plane X′Y ′. To go to the plane, you need to rotate the point by the angle COXA, which we have already calculated earlier.

$$$$ display $$ x ′ = x ′ ⋅ cos (α) + y ′ ⋅ sin (α) = 176.78 cos (-11) + -20 sin (-11) = 180.28 $$ display $$

$$

$$y ′ = y = -20$$

The coordinate y ′ does not change, as we perform the rotation along the axis Y ′.

Then you need to remove the length of COXA from the calculation, i.e. let's move to the X′′Y ′ ′ plane, to do this, we shift the x- coordinate of the point by the length of COXA:

$$

$$x ′ ′ = x ′ - coxaLength = 180.28 - 40 = 140.28$$

$$

$$y ′ ′ = y ′$$

After all these manipulations, the further solution of the problem is reduced to finding the angles a and b of the triangle:


Before finding the angles, you must find the third side C of this triangle. This distance is nothing more than the length of the vector and is calculated by the formula:

$$$$ display $$ C = \ sqrt {x ′ ′ ^ 2 + y ′ ′ ^ 2} = \ sqrt {140.28 ^ 2 + (-20) ^ 2} = 141.70 $$ display $$

Now you need to check whether the limb can reach this point. If C is greater than the sum of the lengths of FEMUR and TIBIA, then the point is not attainable. In our case, 141.70 <141 + 85 - the point is reachable.

Now we know all sides of the triangle and we can find the angles a and b we need using the cosine theorem:

$$

$$a = acos ({A ^ 2 + C ^ 2 - B ^ 2 \ over 2AC}) = 72.05 °$$

$$

$$b = acos ({B ^ 2 + A ^ 2 - C ^ 2 \ over 2BA}) = 72.95 °$$

The angles obtained are not applicable for feeding them to servo drives, since the initial position and the angle of inclination of the straight line C to the X axis are not taken into account here. known. You can find it using the function atan2 (y ′ ′, x ′ ′):

$$$$ display $$ φ = atan2 (y ′ ′, x ′ ′) = atan2 (-20, 140.28) = -8.11 ° $$ display $$

Finally, we can calculate the angle of rotation of the FEMUR and TIBIA servos:

$$

$$FEMUR = femurZeroRotate - a - φ = 135 - 72.05 + 8.11 = 71.06 °$$

$$

$$FEMUR = b - tibiaZeroRotate = 45 - 72.95 = 27.95 °$$

Let's check our calculations:


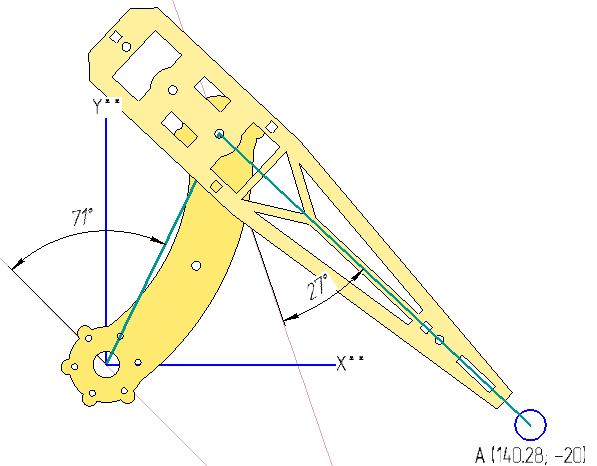
It seems to be true.

Total

The calculated angles of COXA, FEMUR and TIBIA are suitable for feeding them to servos. You may notice that the angle of COXA is negative and, accordingly, the question arises: "How to turn the drive by -11.3 degrees?". The trick is that I use the neutral position of the COXA servo as a logical zero, this allows the drive to be rotated both at positive angles and negative. This is of course obvious, but I think it would not be superfluous to mention this. I will tell about it in more detail in the following articles, when I will talk about the implementation of all the above mentioned.

Sources

Algorithm in action

It was a random sequence that resembled a dance.

PS

I would be glad if someone could simplify this algorithm. I did it so as to understand it later, say, half a year.