📜 ⬆️ ⬇️

Mathematical model of the Dobbl game

Reading difficulty levels



Introduction and rules of the game


A few years ago, I bought the Dobble game ( Dobble , the original name “Spot It!”). This is a very simple, fast and fun game, which I consider to be one of the best board games in general.


The game includes 55 cards with 8 different symbols on each. Here’s what these cards look like:



Fig. 1. An example of the game cards.


For every two cards there is one and only one character. In the above figure, this is a pencil symbol:



Fig. 2. Matching characters on the cards.


The player who first saw the match makes an action with one of the cards, depending on the round of the game. For example, he takes it to himself or throws up his opponent.
Often this leads to the fact that one of the cards for which players are looking for matches, is changing. Because of this, one has to look for a new coincidence, which may be a completely different symbol:




Fig. 3, 4. The first card is replaced with a new one. Now between them is a new coincidence - the symbol of the clown.


How do they do it?


At first glance, it seems incredible that there is exactly one match on two cards, no more, no less. Immediately questions arise - how many characters are there in the game? There cannot be too few of them (then there will be more than one coincidence on the cards) or too many (then there may be no coincidence on the cards at all).
In addition, it is obvious that the symbols are arranged on the cards in a special order, which guarantees the only match for any two cards.


Elementary Google skills lead us to stackoverflow, which describes why this happens: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game


The game uses the principles of finite geometry . Although this phrase has the word "geometry", this concept refers more to combinatorics than to geometry. It operates with a finite number of points, which can be located, in particular, in the form of a projective plane .


Cards and symbols in the game are elements of the projective plane of the 7th order. This means that on each card n + 1 symbol, and the total number of unique symbols in the game is n ^ 2 + n + 1 , i.e. 57 characters.


There are planes of both lower and higher orders. For example, there is a 5 order plane. For it, there are 6 symbols on the card, and the total number of unique symbols in the game is 5 ^ 2 + 5 + 1 = 31. The projective plane of this configuration is used in a simpler version of the Dobl game called Dobl 1,2,3 .


The relationship between points and lines for a projective plane is defined using an incidence matrix . Its appearance is presented in the section “The Incidence Matrix for the Dobbl Game”.


Ultimate geometry for babies


Much later, after writing the original article, I attended a lecture by Alexey Savvateev , where he spoke about projective geometry much shorter and clearer. But since I do not have the strength or desire to rewrite half of the article because of this, I simply recommend his book "Mathematics for the Humanities" if my attempt by the savage to explain the structure of the car on the fingers is incomprehensible or boring.


First, let's go to Wikipedia and read several articles. The first article describes the concept of finite geometry:


Finite geometry is any geometric system that has a finite number of points . [one]

So far, everything is simple. If a pen on paper draws a few points, then they will already make up some final geometry.
Further surprise awaits many:


For example, the Euclidean geometry is not finite, since the Euclidean straight line contains an unlimited number of points, more precisely, it contains exactly as many points as there are real numbers . [one]

For us, this means that the piece of paper on which our points are drawn is not a plane in terms of final geometry . It is just a carrier of points.


There are two types of geometry on the plane: affine and projective . In affine geometry, the usual notion of parallelism of straight lines is used. [one]

Recall the axioms of affine geometry:


Affine geometry on a plane is a non-empty set X (whose elements are called "points"), with a non-empty set L of subsets of X (whose elements are called "straight line"), such that:

  1. For two different points, there is only one straight line that contains both points.
  2. For a line ℓ and a point p that does not belong to существует, there is one and only one straight line ′ ′ containing p such that ℓ ∩ ℓ ′ = ∅.
  3. There are many of four points, no three of which lie on one straight line. [one]

These axioms enable us to understand what the simplest affine plane looks like in finite geometry:


The simplest affine plane contains only 4 points, and is called a second-order affine plane . Each pair of points defines a unique straight line, therefore the indicated plane contains 6 straight lines. [one]

Not very clear? That's right. If you look at the definition of affine geometry, then you can see that it operates with the concepts of set theory (element, set, subset).
This means that straight lines may not look like the usual straight lines of Euclidean geometry.


In fact, it is. If you look at the drawing of the second-order affine plane, we will see the following picture:


Order 2 affine plane


Fig. 5. The affine plane of the second order. (Source ru.wikipedia.org )


The points here look like ordinary black points, but the straight lines are colored segments. Straight lines of the same color are considered parallel.


It is easy to see that the lines here are not of infinite length. In secret I will say that the concept of length is not here at all, and straight lines can have any shape, as we will soon see.


Surely,% username% still doubts that the image of this plane satisfies the axioms of affine geometry. Let's check:


  1. We take 2 any points, for example, the left upper and left lower.
    Both of these points contain only one left red line.
    The right red line does not contain any of these points, and the other straight lines contain only one of them.
  2. Take the left red line and the right upper point. Obviously, only one straight (right red) is parallel to the left red straight line, since it passes through the upper right point, but does not pass through any of the two left points.
  3. The figure clearly shows that no matter what 3 points we take, one of them lies on a line that is different from the line on which both other points lie.
    The two straight lines that make up the diagonal of a square do not intersect, since they have no common points.

If you understand the content of the previous picture, then the picture is more complicated:


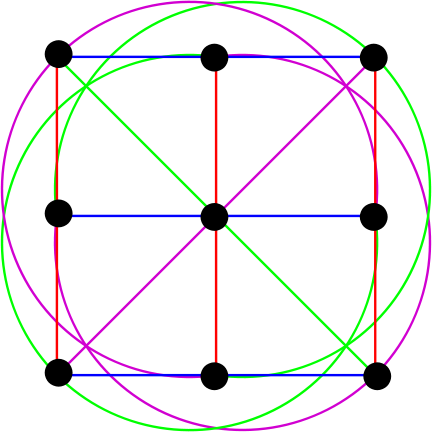
Order 3 affine plane


Fig. 6. The affine plane of the third order. (Source ru.wikipedia.org )


Here we see 9 points and 12 lines. Yes,% username%, these ellipses are actually straight lines in terms of finite geometry.
The figures of the same color are parallel straight lines. They are difficult to notice, so we divide the image into several:


Plane number 1Plane number 2Plane number 3Plane number 4

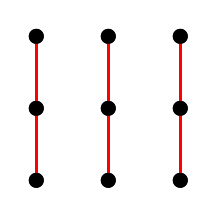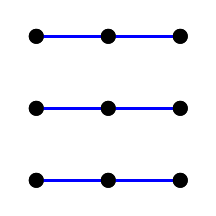Fig. 7. Parallel straight lines of the third order affine plane.


Here, checking the fulfillment of axioms will take a little more time:


  1. We take 2 any points, for example, the upper center and lower right. Only one of the purple lines passes through them.
  2. Take the left red line and the right lower point. Similar to the plane of the second order, only one right red line passes through this point, but does not pass through any of the three left points.
  3. Here is a little more complicated than in the case of a 2-order plane. The formulation of the axiom says that you need to find at least one (non-empty) set of four points in which no three lie on more than one line.
    Obviously, 12 sets with three points through which the lines in the figure pass do not satisfy this condition. But he is satisfied, for example, with a set of four corner points.

In the more general case, a finite affine plane of order n has n ^ 2 points and n ^ 2 + n lines; each line contains n points, and each point belongs to n + 1 lines. [one]

We finished with affine geometry, go to the second type of geometry on the plane - projective.


In projective geometry, on the contrary, any two straight lines intersect at the only possible point, and therefore there are no parallel straight lines. [one]

The previous sentence describes the second axiom of projective geometry. The first and third are the same as in the affine.


Since the third axiom requires the existence of at least four points, the plane must contain at least 7 points in order to satisfy the conditions of the first two axioms. In this simplest of projective planes there are also 7 straight lines; each point belongs to three straight lines, and each straight line contains three points. Such a projective plane is often called the “Fano plane” . [one]

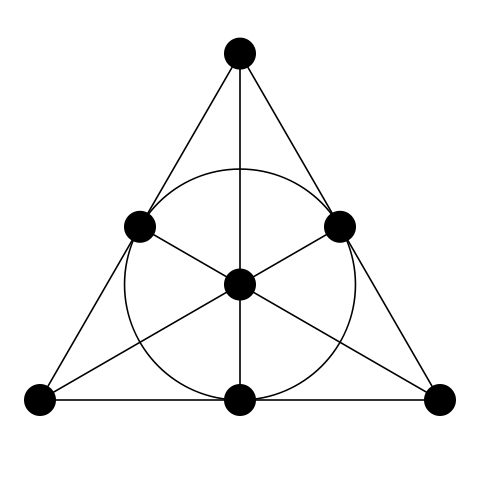
Fano plane
Fig. 8. Fano plane. (Source en.wikipedia.org )


In this picture it is difficult to immediately disassemble all 7 lines, so here's a pony version of the same plane:



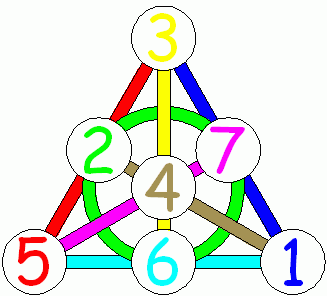
Fig. 9. Fano plane with colored lines. (Source mathpuzzle.com . Used with permission from Ed Pegg Jr. )


So, the Fano plane is a 2-order projective plane with 7 points and 7 lines.


What does the card?


What will happen if we reformulate the 2 axioms of finite geometry , replacing the “straight line” with “symbol” and “point” with “card”?


It turns out this:


  1. For two different cards, there is only one character that is shown on both cards.
  2. For two different symbols, there is only one card that contains both of these symbols.

Now, on the basis of this knowledge, let's see what Dobble would look like in the simplest case. In it there would be 7 cards and 7 symbols, on each card there would be 3 symbols (since 3 straight lines intersect at one point):



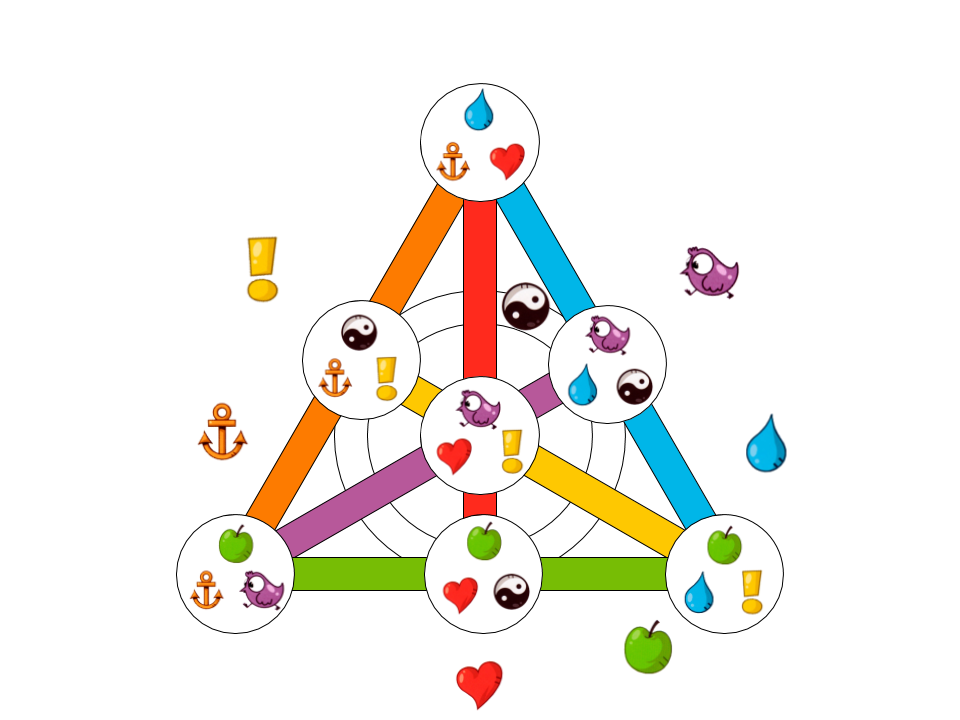
Fig. 10. An example of the minimum possible set of cards for Dobble.


The following 7 characters are used here:


, , , , , ,
Whatever 2 cards we take, they will have a common symbol, depicted next to the line on which both cards lie.
For example, the card in the lower left corner and the card in the middle of the right side have a common symbol . He is depicted next to the straight .


Small projective planes


A visual demonstration of small-order projective planes can be found on the Wolfram website: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
It is framed as a document in CDF (Computable Document Format) format, for which you need to install CDF Player .


Here is an example of a projective plane of order 3:



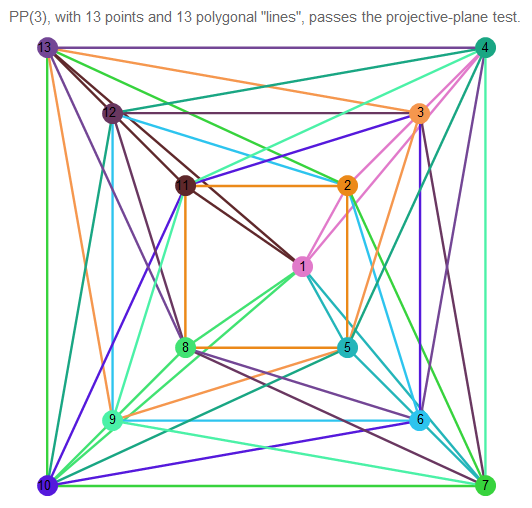
Fig. 11. The image of the projective plane 3 order.


It is difficult to understand what is happening, so take 2 arbitrary lines:



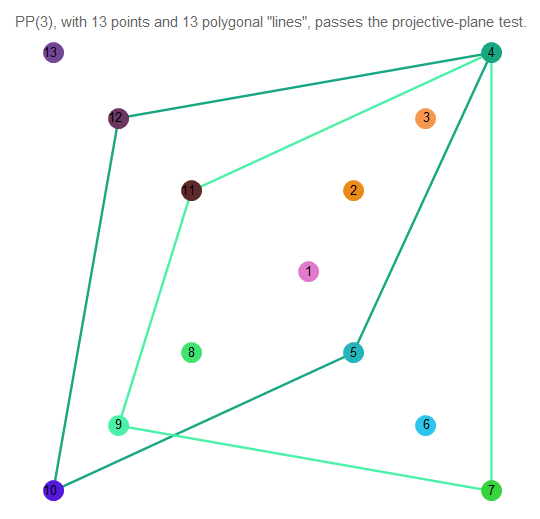
Fig. 12. The intersection of two lines of the projective plane of 3 order.


As we see, they intersect at exactly one point. The lines themselves contain 4 points each.


To make sure that 4 straight lines pass through each point, you have to switch the displayed pairs of straight lines in an interactive document and focus on a particular point.


Projective planes of higher orders are depicted in the figures below.



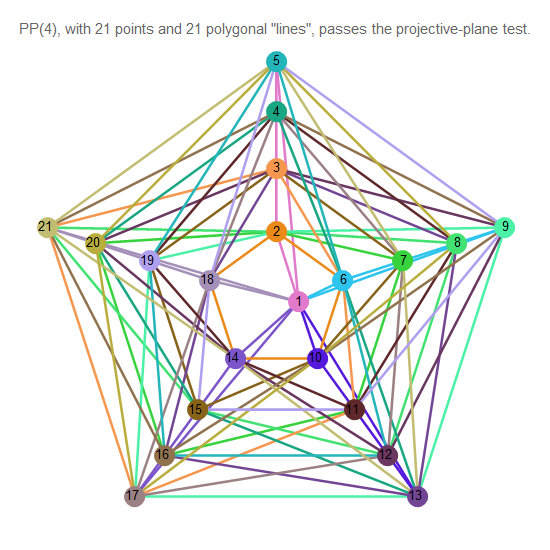
Fig. 13. Projective plane of order 4



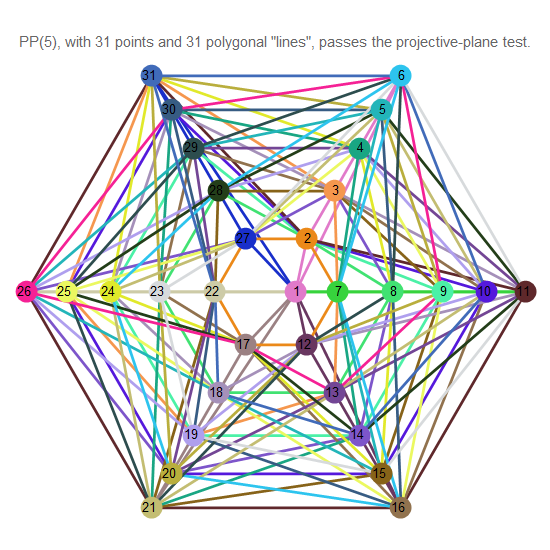
Fig. 14. Projective plane of order 5



Fig. 15. Projective plane of order 7


In the given sequence there is no image for the 6th order projective plane. It's not a mistake.


Although Wolfram generates a graphical representation of such a structure, it does not satisfy the axioms of projective geometry, and is not a projective plane.


It is assumed, but still not proven, that the order of the final plane is always a power of a prime number . [one]


How to build a projective plane?


The graphical representation of the projective plane looks interesting and clear, but how to find such a combination of points so that it has the above properties?


The easiest way is to visit sites where the calculated data for projective planes of different orders are placed.


For example, for the projective plane of order 7, you can visit this page: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
There is a matrix of numbers. Strings are cards (dots) in terms of Dobble. The numbers in the lines are the ordinal numbers of the characters (lines), starting with zero, which are drawn on each card (pass through the given point).


You can also use the services of mathematical packages, such as Matlab, to build the incidence matrix of the projective plane. [2] [3]


Incidence Matrices


The incidence matrix is one of the forms of representation of the graph , in which the links between the incident elements of the graph (edge ​​(arc) and vertex) are indicated. The columns of the matrix correspond to the edges, the rows - to the vertices. A non-zero value in the matrix cell indicates the relationship between the vertex and the edge (their incidence ). [2]

One of the simplest examples of an incidence matrix can be a 2x1 matrix for an undirected graph of two vertices connected by one edge:



Fig. 16. The undirected graph of two vertices connected by one edge, and its incidence matrix.


A more complex example of a graph and its incidence matrix:



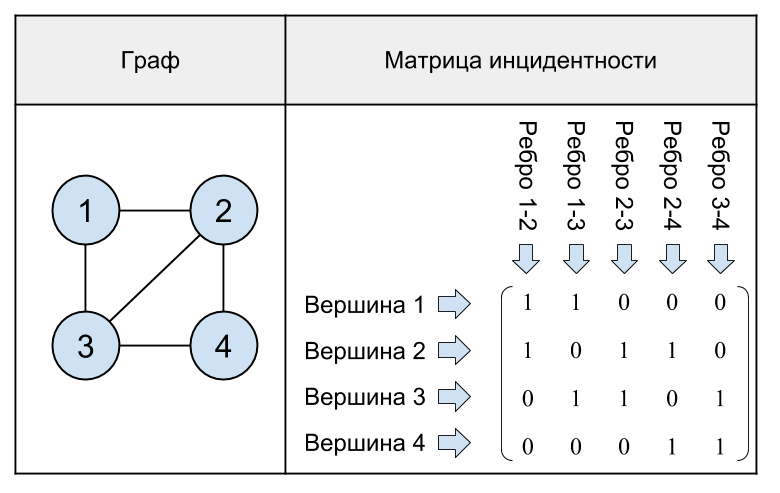
Fig. 17. A non-oriented graph with 4 vertices and its incidence matrix.


As can be seen from the last example, in the incidence matrix of the graph there are exactly two units in each column, since one edge connects two vertices.
The projective plane is a hypergraph , since one straight line (edge) connects several points (vertices). Therefore, in the incidence matrix of the projective plane, the units in each column occur n + 1 times, where n is the order of the projective plane.


For the Fano plane shown in fig. 9, the incidence matrix will be as follows:



Fig. 18. The incidence matrix of the Fano plane.


To simplify the perception, the zeros are not shown, and the units are replaced with the X character.
In this representation of the projective plane, the principle of duality of points and straight lines is clearly noticeable - the straight line passes through exactly 3 points, and, at the same time, the point belongs to exactly three straight lines.


Build the projective plane through brute force


Current knowledge of the properties of the incidence matrix is ​​sufficient to construct it for a projective plane of any order n. You can use the following pseudocode for this:


Для всех столбцов Для всех строк Если в столбце стоит n+1 единиц, то перейти к следующему столбцу Если в строке стоит n+1 единиц, то перейти к следующей строке Для каждого предыдущего столбца Х Если в столбце Х на текущей строке стоит единица и Если уже есть совпадения в строках для столбца Х и текущего столбца, то перейти к следующей строке Поставить единицу Перейти на следующую строку Перейти на следующий столбец

Following this algorithm, we get a symmetric matrix for the Fano plane:



Fig. 19. The incidence matrix of the Fano plane, built on the pseudo-code algorithm.


This matrix does not coincide with the previous one. In fact, it does not matter.
Rearranging any two rows of the incidence matrix is ​​equivalent to renumbering the vertices of the graph.
Rearranging any two columns of the incidence matrix is ​​equivalent to renumbering the edges of the graph (if we number them in advance).


Dobble Incident Matrix


For the Dobbl game in the incidence matrix, the rows are responsible for the cards, and the columns for the symbols on them.
Thus, the permutation of any two columns of the incidence matrix is ​​equivalent to a change in the sequence of the characters on the card. However, the characters on the card are unordered, so this operation does not affect the appearance of the cards.
Swapping the two lines means that on all the cards two corresponding characters replace each other.


The last operation changes the appearance of the cards, which means that the character set that we see in the game is just one of the possible combinations.
The number of character sets for a single card is a combination of no repetitions of 57 elements by 8 elements. It is calculated by the formula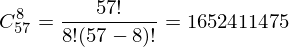


The incidence matrix for the Dobbl game is shown in the table below. It is transposed, i.e. rows are symbols, and columns are cards (the image is clickable). Habr does not allow you to insert a picture of the desired size and quality, so full option is a separate link: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png



Fig. 20. The matrix of incidence of the Dobbl game.


What two cards are missing in the game bundle?


In total, the table with the incidence matrix of the game has 57 rows and 55 columns. This means that there could be 2 more cards in the game.
This means that the symbols that should be on these cards are less common in the game than the rest. The number of characters in the game is shown in the last column of the table.


The number of characters from the missing cards is as follows:



What do the missing cards look like? To answer this question, take any of the above symbols in the incidence matrix (except for the snowman), and place it on the missing card (for example, the penultimate column).


Then we find all the cards (columns) on which this symbol is depicted. This means that on all these cards the characters are the same, and there can be no other matches.


Since these cards already have a match with the selected symbol, we delete all the symbols that appear on the remaining cards from the last column.
Missing characters that were not crossed out, and make up the symbols of one of the remaining cards. Since they turned out exactly 8, the type of the second missing card is determined unequivocally.


These 2 cards are:



Fig. 21. Possible type of missing cards №56 and №57.


It remains to answer the last question - does the absence of these cards affect the coincidence property of a single character between two cards (i.e. suddenly there are no matches between some cards)?


The answer is obvious, if you still look at the game's incidence matrix - no, it does not. There is still only one match between any two cards (columns).


Why is the game 2 cards less than the maximum possible amount?


Initially, the rules for five mini-games were not in the booklet, but on five separate cards. At the same time, the maximum could be printed only 60 cards. Therefore, the authors of the game decided to remove 2 cards so that in the end they got 55 cards with symbols + 5 cards with rules. (Special thanks to Guillaume Gille-Naves for the clarification).


Thanks


I express my deep gratitude to the network of stores of board games “Igroved” for help in writing the article.
Thanks to Ed Pegg Jr for the provided image of the Fano plane.
Separately, I want to mention one Anonymous and Master for help in checking the article.
I thank the store "Desktop Grad" for help in preparing for the publication of the article.
From the bottom of my heart, I thank the authors of the game Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves, and the company Asmodee for the right to use images from the game.



Source: https://habr.com/ru/post/437140/

More articles: