Ticket to Ride. Europe - arithmetic, part two
Still continuing to learn the basics of mathematics and mechanics in the game. This article is the second in the series ( Link to the first part ), it continues the analysis of the hauls, an attempt to sort them according to needs, the study of various ways to build routes. If we draw analogies with mathematics, these are just the basics, arithmetic. Algebra and higher mathematics in the spirit of “taking wagons or building a stage?”, “What is better to build now — stage or station?” And “using one route by several routes” while in the planning stage, I hope, hands and brains will reach them.
By default, there are arguments in the post, 2-3 players relevant for the game (only one path is used on “double-track” runs)
As the practice of the game and comments from respected participants show, the shortest path between the two cities is not always the most profitable ( to be extremely honest, it is almost never ). Let's try to find a way where the ratio of "points earned / spent moves" would be the maximum.
The algorithm turned out to be rather slow, for each card of the route it “wool” all possible options for about one and a half minutes, while consuming 3 gigabytes of RAM.

The most "profitable" routes and routes for them
The results of the execution of the algorithm sometimes gave completely "illogical" in human opinion results. For example, the route "London-Berlin" (7 points), the computer proposes to build in this way: " London-Dieppe-Paris-Marseille-Rome-Palermo-Smyrna-Constantinople-Bucharest-Budapest-Kiev-Warsaw-Berlin " (average 101 move; 81 points for constructed legs).
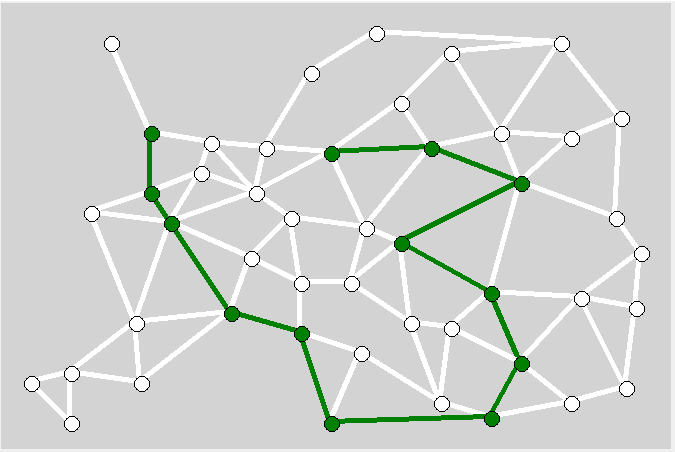
As my grandfather, a front-line soldier, said: “From Kiev through Penza, to Zhytomyr”
After the list of the most "profitable" routes is formed, you can proceed to the next stages of calculation.
As in the previous time, for each city, the number of routes in which it participates was calculated (as the final station and as an intermediate one). "Workload" was considered as the difference between the ways from the city / to the city and the number of routes.

The busiest cities

The most "free" cities
When calculating the workload of cities, only the number of hauls approaching the city was taken into account, the number of tracks in the haul (one or two) was ignored. Accordingly, the numbers are more or less relevant for the game together or three of us. Well and ... the tables in themselves do not carry any useful information, unless they help to choose from which city to begin construction with other things being equal. Much more important information on the stage.
Like last time, the most “profitable tracks” were analyzed, the use of spans in them was calculated, regardless of the direction of movement (that is, movements like “London-Edinburgh” and “Edinburgh-London” are considered as movements according to the same same distilled).

The busiest hauls, they need to occupy first

Transit that was not used for the construction of routes
In the comments to the last entry, pproger and g000phy wrote that in order to win the game, use 8 and 6 wagon lengths. As expected, the 6-carriages “Kiev-Budapest” and “Palermo-Smyrna”, as well as access roads to them, are at the top of the “busiest” table. Unexpectedly, but Stockholm-Petrograd was at the bottom of the Top-10 rating. Apparently, it affects its remoteness from the main routes and a large number of cars that should be spent on construction.

Heat map. The farther from the green, the more loaded this stage / city. White marked unused paths.
In the comments to the previous entry, woozle wrote about the key hauls, the lack of which would lead to an increased consumption of cars and moves (a striking example is the “Kharkov-Rostov” stage for the eastern segment).
On the process of finding these hauls would like to ask for advice from a respected community.
I see the search algorithm as follows:
Currently, there are two options of the “route” for each route:
Actually, the search for "key" hauls abuts against a set of primary data (a list of logically constructed routes). These “logical routes” are not at hand, there are no ideas - how to find them. I would appreciate thoughts and suggestions.
Continuation (station, the longest way) follows ...
By default, there are arguments in the post, 2-3 players relevant for the game (only one path is used on “double-track” runs)
Brief information about the first part
In the first article, with the help of python and Excel, an attempt was made to understand which cars it would be more profitable to use for the construction of "gray" hauls, how to quickly build one route or another.
From the previous developments, only the table “number of moves for the construction of the leg N” will be used:

From the previous developments, only the table “number of moves for the construction of the leg N” will be used:

Search for the most "profitable" way
As the practice of the game and comments from respected participants show, the shortest path between the two cities is not always the most profitable ( to be extremely honest, it is almost never ). Let's try to find a way where the ratio of "points earned / spent moves" would be the maximum.
Description of the path finding algorithm
1. For each of the 46 route cards, a search is made for all possible “tracks” from the starting point to the destination. For the “routes” of the routes we introduce two restrictions:
All this is implemented with the help of the standard search "in depth".
2. Of all the possible "tracks" is chosen the one for which the ratio
(Points for the runs + Points for the routes) / (Number of moves spent)
is the greatest.
- The length (the number of wagons spent) does not exceed 45 (the maximum possible cars).
- Each city can be used only once (loops are not considered).
All this is implemented with the help of the standard search "in depth".
2. Of all the possible "tracks" is chosen the one for which the ratio
(Points for the runs + Points for the routes) / (Number of moves spent)
is the greatest.
The algorithm turned out to be rather slow, for each card of the route it “wool” all possible options for about one and a half minutes, while consuming 3 gigabytes of RAM.

The most "profitable" routes and routes for them
The results of the execution of the algorithm sometimes gave completely "illogical" in human opinion results. For example, the route "London-Berlin" (7 points), the computer proposes to build in this way: " London-Dieppe-Paris-Marseille-Rome-Palermo-Smyrna-Constantinople-Bucharest-Budapest-Kiev-Warsaw-Berlin " (average 101 move; 81 points for constructed legs).

As my grandfather, a front-line soldier, said: “From Kiev through Penza, to Zhytomyr”
After the list of the most "profitable" routes is formed, you can proceed to the next stages of calculation.
Search for the busiest cities
As in the previous time, for each city, the number of routes in which it participates was calculated (as the final station and as an intermediate one). "Workload" was considered as the difference between the ways from the city / to the city and the number of routes.

The busiest cities

The most "free" cities
When calculating the workload of cities, only the number of hauls approaching the city was taken into account, the number of tracks in the haul (one or two) was ignored. Accordingly, the numbers are more or less relevant for the game together or three of us. Well and ... the tables in themselves do not carry any useful information, unless they help to choose from which city to begin construction with other things being equal. Much more important information on the stage.
Most loaded hauls
Like last time, the most “profitable tracks” were analyzed, the use of spans in them was calculated, regardless of the direction of movement (that is, movements like “London-Edinburgh” and “Edinburgh-London” are considered as movements according to the same same distilled).

The busiest hauls, they need to occupy first

Transit that was not used for the construction of routes
In the comments to the last entry, pproger and g000phy wrote that in order to win the game, use 8 and 6 wagon lengths. As expected, the 6-carriages “Kiev-Budapest” and “Palermo-Smyrna”, as well as access roads to them, are at the top of the “busiest” table. Unexpectedly, but Stockholm-Petrograd was at the bottom of the Top-10 rating. Apparently, it affects its remoteness from the main routes and a large number of cars that should be spent on construction.

Heat map. The farther from the green, the more loaded this stage / city. White marked unused paths.
Overdrive top priority
In the comments to the previous entry, woozle wrote about the key hauls, the lack of which would lead to an increased consumption of cars and moves (a striking example is the “Kharkov-Rostov” stage for the eastern segment).
On the process of finding these hauls would like to ask for advice from a respected community.
I see the search algorithm as follows:
- The number of moves required for the construction of each route is summed up (a certain standard is obtained).
- Each route is alternately excluded from the matrix of paths. Again, the amount of moves spent on each route is considered.
- The “importance” of each span is considered as the difference between the spent moves for the removed span and the standard.
Currently, there are two options of the “route” for each route:
- The route from point A to point B in the least number of moves . The algorithm is described in the previous article, the result of the importance calculation is given below:

“Edinburgh-London” is not listed (if one player builds the cars on this route, the second one will set up the station or remain with an incomplete route). The importance of the “Copenhagen-Essen”, “Stockholm-Copenhagen” and “Kharkiv-Rostov” hauls is also obvious, but the others on the list raise doubts ... - The route from point A to point B with the highest ratio "the number of points received / the number of moves spent . " For this case, critical runs were not considered for two reasons. First, long (90 spans * 46 routes * 1.5 minutes per count). Secondly, the laid "routes" of routes give such "rounds" that for the most part are unlikely to be used in a real game.
Actually, the search for "key" hauls abuts against a set of primary data (a list of logically constructed routes). These “logical routes” are not at hand, there are no ideas - how to find them. I would appreciate thoughts and suggestions.
Continuation (station, the longest way) follows ...
Source: https://habr.com/ru/post/439020/