📜 ⬆️ ⬇️

Julia, Gradient descent and simplex method


We continue our acquaintance with the methods of multidimensional optimization.


Further, the implementation of the method of fastest descent with the analysis of the speed of execution, as well as the implementation of the Nelder-Mead method by means of the Julia and C ++ language, are proposed.


Gradient descent method


The search for extremum is conducted in steps in the direction of the gradient (max) or anti-gradient (min). At each step in the direction of the gradient (antigradient), the movement is carried out as long as the function increases (decreases).


Follow the theory to follow the links:



The model function will choose an elliptical paraboloid and set the relief drawing function:


using Plots plotly() # интерактивные графики function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) # линовка осей yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end parabol(x) = sum(u->u*u, x) # сумма квадратов fun = parabol plotter(surface, low = [-1 -1], up = [1 1])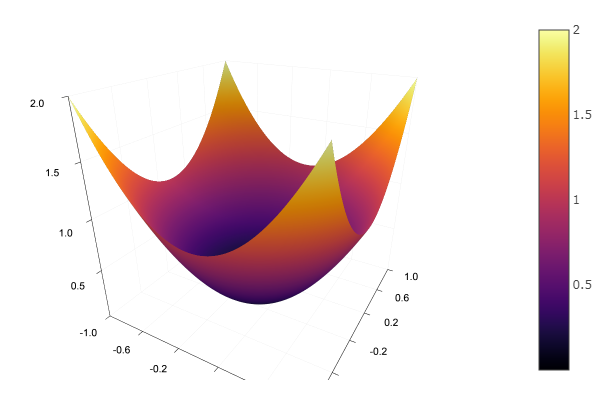


Let us set a function implementing the method of steepest descent, which takes the dimension of the problem, the accuracy, the step length, the initial approximation, and the size of the bounding box:


 # точка-с-запятой значит, что все последующие параметры - ключевые слова function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) end #println(fun(fit)) end

On the function of calculating the direction of the gradient can be sharpened in terms of optimization.


The first thing that comes to mind is actions with matrices:


 # \delta - приращение аргумента используемое для вычисления # производных по формуле центральных разностей function grad(fit, δ) ndimes = length(fit) Δ = zeros(ndimes, ndimes) for i = 1:ndimes Δ[i,i] = δ end fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes] fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes] g = 0.5(fr - fl)/δ modg = sqrt( sum(x -> x*x, g) ) g /= modg end

What makes Julia really good is that problem areas can be easily tested:


 #]add BenchmarkTools using BenchmarkTools @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 44.14 KiB allocs estimate: 738 -------------- minimum time: 76.973 μs (0.00% GC) median time: 81.315 μs (0.00% GC) mean time: 92.828 μs (9.14% GC) maximum time: 5.072 ms (94.37% GC) -------------- samples: 10000 evals/sample: 1

You can rush to reprint everything in Cishny style


 function grad(fit::Array{Float64,1}, δ::Float64) ndimes::Int8 = 2 g = zeros(ndimes) modg::Float64 = 0. Fr::Float64 = 0. Fl::Float64 = 0. for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= 2δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ modg += g[i]*g[i] end modg = sqrt( modg ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 14.06 KiB allocs estimate: 325 -------------- minimum time: 29.210 μs (0.00% GC) median time: 30.395 μs (0.00% GC) mean time: 33.603 μs (6.88% GC) maximum time: 4.287 ms (98.88% GC) -------------- samples: 10000 evals/sample: 1

But as it turns out, it itself and without us knows which types should be put, so we arrive at a compromise:


 function grad(fit, δ) # вычисляет направление градиента ndimes = length(fit) g = zeros(ndimes) for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= δ fit[i] -= δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ end modg = sqrt( sum(x -> x*x, g) ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 15.38 KiB allocs estimate: 409 -------------- minimum time: 28.026 μs (0.00% GC) median time: 30.394 μs (0.00% GC) mean time: 33.724 μs (6.29% GC) maximum time: 3.736 ms (98.72% GC) -------------- samples: 10000 evals/sample: 1

And now let him draw:


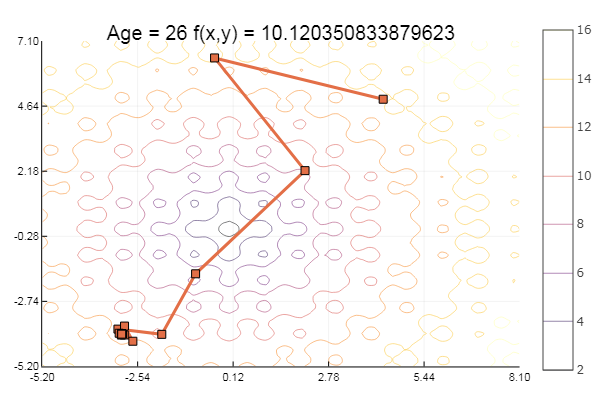
 function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) plotter(contour, low = low, up = up) while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) push!(x, fit[1]) push!(y, fit[2]) end plot!(x, y, w = 3, legend = false, marker = :rect ) title!("Age = $kf(x,y) = $(fun(fit))") println(fun(fit)) end ofGradient()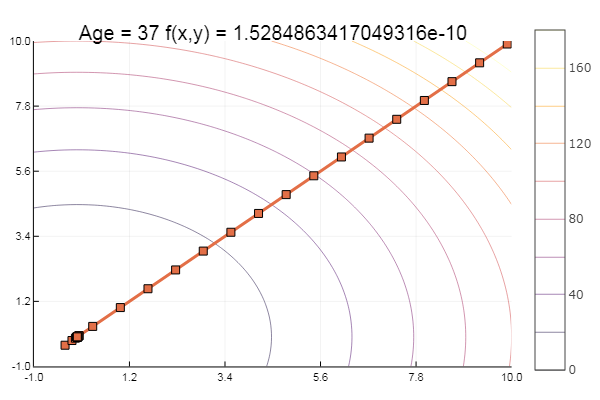


And now let's test on Ackley's functions:


 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )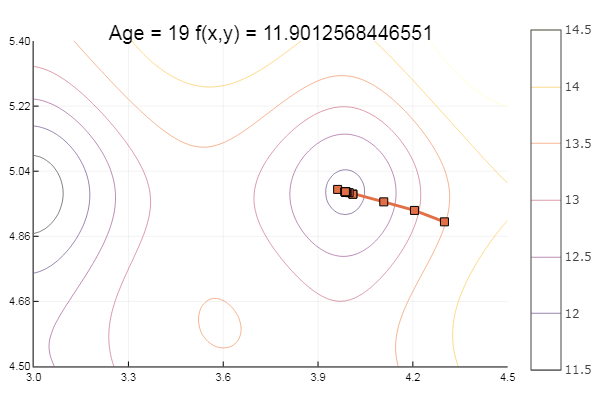


Dropped to a local minimum. Let's take more steps:


 ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] )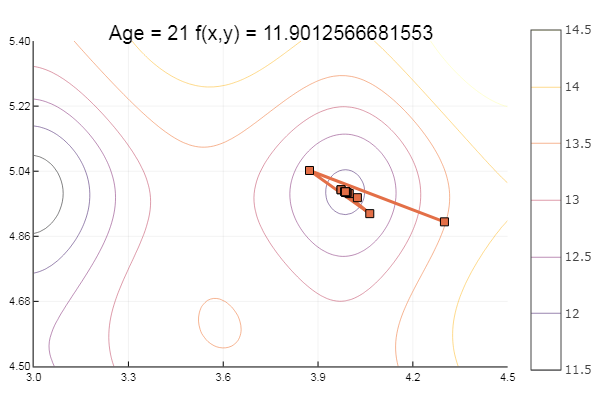 


 ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )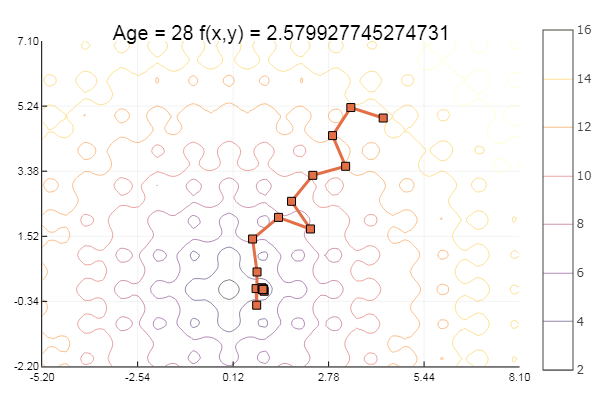


… And a bit more:


 ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )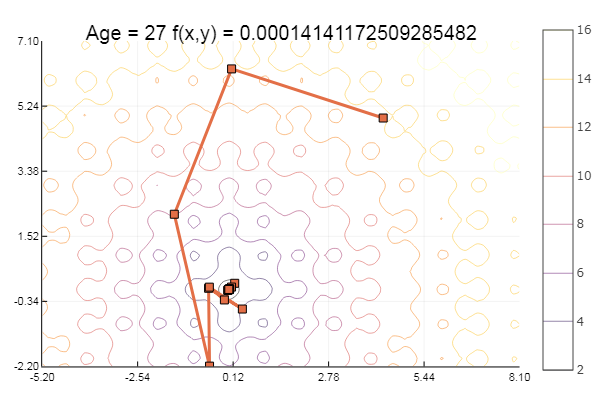


Fine! And now something with a ravine, for example the Rosenbrock function:


 rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] fun = rosenbrok plotter(surface, low = [-2 -1.5], up = [2 1.5])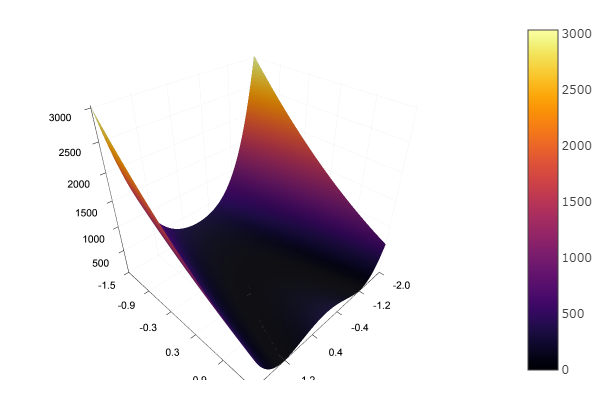 


 ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] )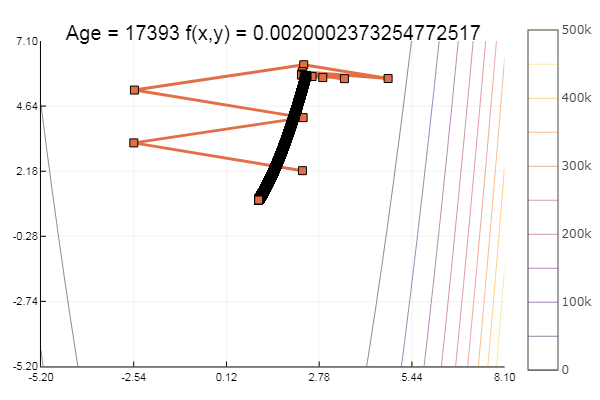 


 ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )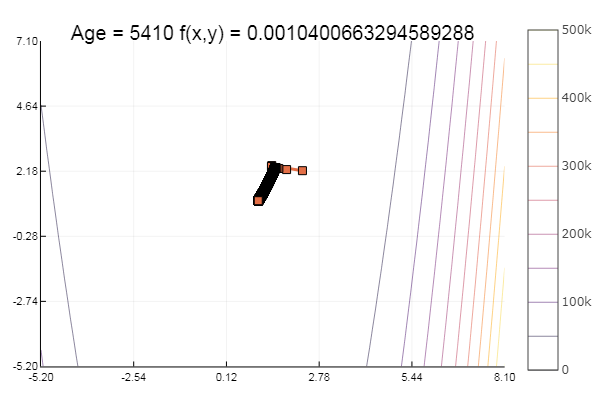


Moral: gradients do not like the slopes.


Simplex method


The Nelder – Mead method, also known as the deformable polyhedron method and the simplex method, is an unconditional optimization method for a function of several variables that does not use the derivative (or more precisely, gradients) function, and therefore is easily applicable to non-smooth and / or noisy functions.


The essence of the method lies in the sequential movement and deformation of the simplex around the extremum point.


The method finds a local extremum and can “get stuck” in one of them. If you still need to find a global extremum, you can try to choose another initial simplex.


Secondary functions:


 #сортировка столбцов матрицы выстраиванием элементов последней строки в порядке возрастания function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] # значение функции в вершинах Mx[:, sortperm(f)] #Return a permutation vector I that puts v[I] in sorted order. end # Норма матрицы function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) vecl(x) = sqrt( sum(u -> u*u, x) )# длина вектора for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) # считает длину разности столбцов end D sqrt(maximum(D)) end function simplexplot(xy, low, up) for i = 1:length(xy) if i%11 == 0 low *= 0.05 up *= 0.05 end Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] contour(Xs, Ys, Zs) xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] ) yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] ) plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle ) title!("Age = $if(x,y) = $(fun(xy[i][:,1]))") savefig("$fun $i.png") end end

And the simplex method itself:


 function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) vecl(v) = sqrt( sum(x -> x*x, v) ) k = 0 N = ndimes dz = zeros(N, N+1) Xx = zeros(N, N+1) coords = [] for i = 1:N+1 Xx[:,i] = fit end for i = 1:N dz[i,i] = 0.5*vecl(fit) end Xx += dz p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] # среднее эл-тов i-й строки Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end #println(k, " ", p, " ", Xx[:,1]) push!(coords, [Xx[:,1:3] Xx[:,1] ]) p = normx(Xx) end #while #simplexplot(coords, low, up) fit = Xx[:,1] end ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])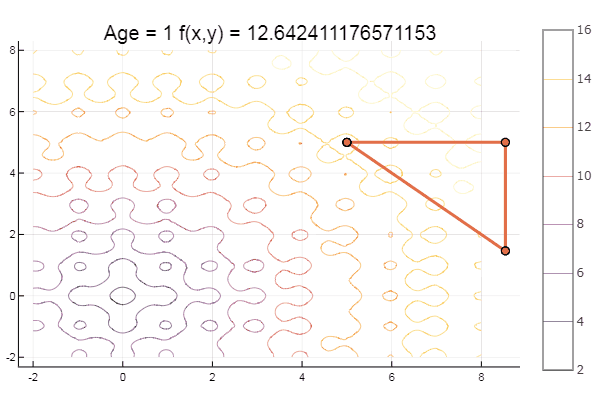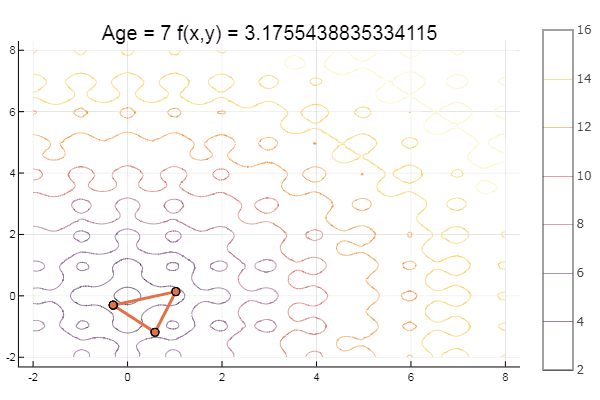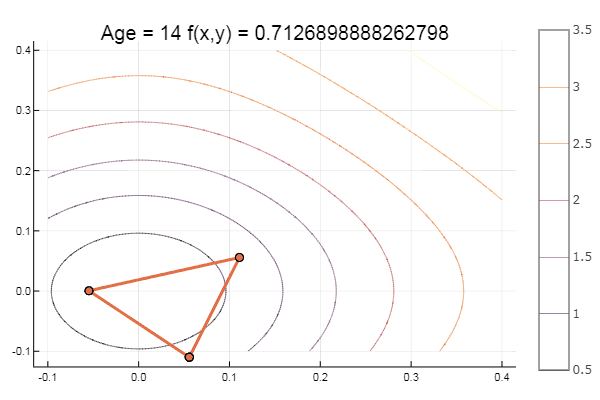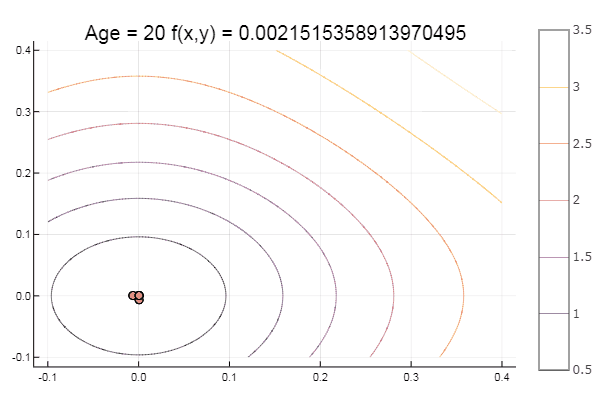


And for dessert, some beech ... for example, the function of Bukin


 bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] fun = bukin6 ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])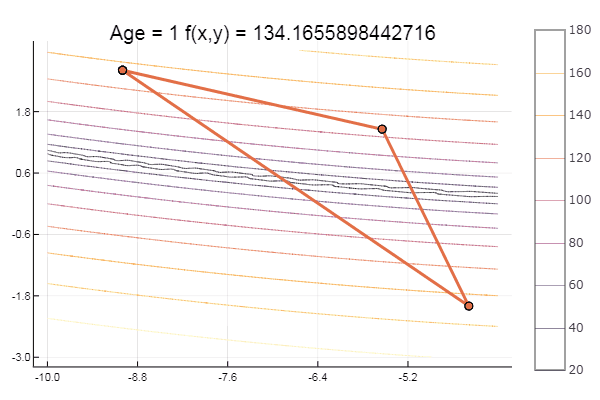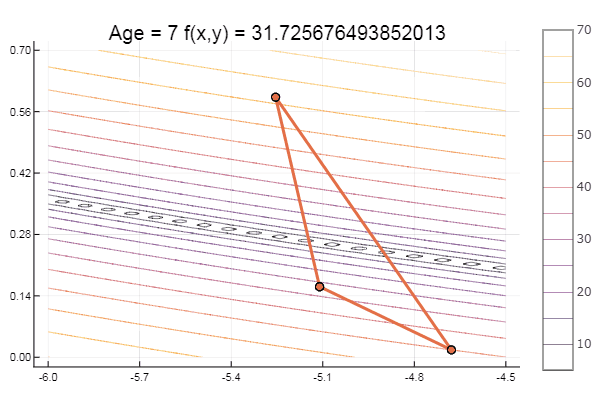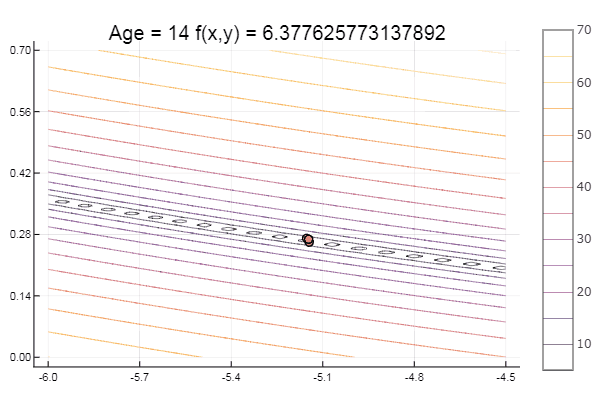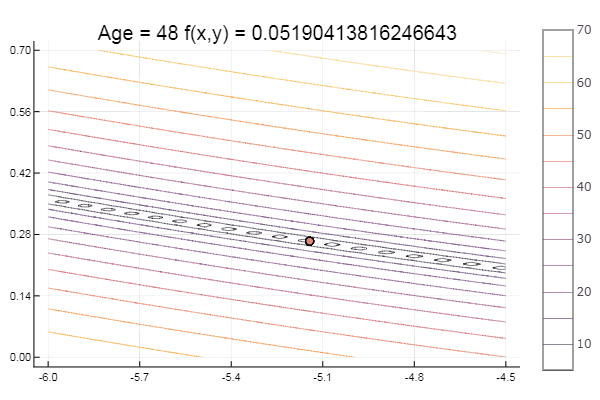


The local minimum is nothing, the main thing is to choose the starting simplex correctly, so for myself I found a favorite.


Bonus Methods of Nelder-Meade, the fastest descent and coordinate descent in C ++


Alarm! 550 lines of code!
 /* * File: main.cpp * Author: User * * Created on 3 сентября 2017 г., 21:22 */ #include <iostream> #include <math.h> using namespace std; typedef double D; class Model { public: D *fit; D ps; Model(); DI(); }; Model :: Model() { ps = 1; fit = new D[3]; fit[0]=1.3; fit[1]=1.; fit[2]=2.; } D Model :: I() // rosenbrock { return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]); } class Methods : public Model { public: void ofDescent(); void Newton(int i); void SPI(int i); //sequential parabolic interpolation void Cutters(int i); void Interval(D *ab, D st, int i); void Gold_section(int i); void ofGradient(); void Grad(int N, D *g, D delta); void Srt(D **X, int N); void ofNelder_Mid(); D Nor(D **X, int N); }; void Methods :: ofDescent()//метод покоординатного спуска { int i, j=0; D *z = new D[3]; D sumx, sumz; sumx = sumz = 0; do { sumx = sumz = 0; for(i=0; i<3; i++) z[i] = fit[i]; for(i=0; i<2; i++) { //Cutters(i); //SPI(i); Newton(i); //Gold_section(i); sumx += fit[i]; sumz += z[i]; } j++; //if(j%1000==0) cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl; //cout << sumz << " " << sumx << endl; } while(fabs(sumz - sumx) > 1e-6); delete[]z; } void Methods :: SPI(int i) { int k = 2; D f0, f1, f2; D v0, v1, v2; D s0, s1, s2; D *X = new D[300]; X[0] = fit[i] + 0.01; X[1] = fit[i]; X[2] = fit[i] - 0.01; while(fabs(X[k] - X[k-1]) > 1e-3) { fit[i] = X[k]; f0 = I(); fit[i] = X[k-1]; f1 = I(); fit[i] = X[k-2]; f2 = I(); v0 = X[k-1] - X[k-2]; v1 = X[k ] - X[k-2]; v2 = X[k ] - X[k-1]; s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2]; s1 = X[k ]*X[k ] - X[k-2]*X[k-2]; s2 = X[k ]*X[k ] - X[k-1]*X[k-1]; X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0); k++; cout << k << " " << X[k] << endl; } fit[i] = X[k]; delete[]X; } void Methods :: Newton(int i) { D dt, T, It; int k=0; while(fabs(T-fit[i]) > 1e-3) { It = I(); T = fit[i]; fit[i] += 0.01; dt = I(); fit[i] -= 0.01; fit[i] -= It*0.001 / (dt - It); cout << k << " " << fit[i] << endl; k++; } } void Methods :: Cutters(int i) { D Tn, Tnm, Tnp, It, Itm; int j=0; Tn = 0.15; Tnm = 2.65;//otrezok Itm = I(); //cout << Tnm << " " << Tn << endl; while(fabs(Tn-Tnm) > 1e-6) { fit[i] = Tn; It = I(); Tnp = Tn - It * (Tn-Tnm) / (It-Itm); cout << j+1 << " " << Tnp << endl; Itm = It; Tnm = Tn; Tn = Tnp; j++; } fit[i] = Tnp; } void Methods :: Interval(D *ab, D st, int i) { D Fa, Fdx, d, c, Fb, fitbox = fit[i]; ab[0] = fit[i]; Fa = I(); fit[i] -= st; Fdx = I(); fit[i] += st; if(Fdx < Fa) st = -st; fit[i] += st; ab[1] = fit[i]; Fb = I(); while(Fb < Fa) { d = ab[0]; ab[0] = ab[1]; Fa = Fb; fit[i] += st; ab[1] = fit[i]; Fb = I(); cout << Fb << " " << Fa << endl; } if(st<0) { c = ab[1]; ab[1] = d; d = c; } ab[0] = d; fit[i] = fitbox; } void Methods :: Gold_section(int i) { D Fa, Fb, al, be; D *ab = new D[2]; D st = 0.5; D e = 0.5*(sqrt(5) - 1); Interval(ab, st, i); al = e*ab[0] + (1-e)*ab[1]; be = e*ab[1] + (1-e)*ab[0]; fit[i] = al; Fa = I(); fit[i] = be; Fb = I(); while(fabs(ab[1]-ab[0]) > e) { if(Fa < Fb) { ab[1] = be; be = al; Fb = Fa; al = e*ab[0] + (1-e)*ab[1]; fit[i] = al; Fa = I(); } if(Fa > Fb) { ab[0] = al; al = be; Fa = Fb; be = e*ab[1] + (1-e)*ab[0]; fit[i] = be; Fb = I(); } cout << ab[0] << " " << ab[1] << endl; } fit[i] = 0.5*(ab[0] + ab[1]); cout << ab[0] << " " << ab[1] << endl; } void Methods :: Grad(int N, D *g, D delta)//вектор направления градиента { int n; D Fr, Fl, modG=0; for(n=0; n<N; n++) { fit[n] += delta; Fr = I(); fit[n] -= delta; fit[n] -= delta; Fl = I(); fit[n] += delta; g[n] = (Fr - Fl)*0.5/delta; modG += g[n]*g[n]; } modG = sqrt(modG); for(n=0; n<N; n++) g[n] /= modG; g[N] = I(); } void Methods :: ofGradient() { int n, j=0; D Fun, st, eps; const int N = 2; D *g = new D[N+1]; st = 0.1; eps = 0.000001; while(st > eps) { Grad(N,g,0.0001); for(n=0; n<N; n++) fit[n] -= st*g[n]; Fun = I(); if(Fun >= g[N]) { st /= 2.; for(n=0; n<N; n++) fit[n] += st*g[n]; } j++; cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl; } } void Methods :: ofNelder_Mid() { int i, j, k; D modz = 0., p, eps = 1e-3; D FR, FN, F0, FE, FNm1, FC; const int N = 2; D *Co = new D[N]; D *Eo = new D[N]; D *Ro = new D[N]; D *Xo = new D[N]; D **Xx = new D*[N]; D **dz = new D*[N]; for(i=0;i<N;i++) { dz[i] = new D[N]; Xx[i] = new D[N+1]; } for(i=0;i<N;i++) for(j=0;j<N;j++) if(i^j) dz[i][j] = 0; else dz[i][j] = 1; for(i=0;i<N;i++) Xx[i][N] = fit[i]; for(i=0;i<N;i++) modz += fit[i]*fit[i]; modz = sqrt(modz); for(i=0;i<N;i++) dz[i][i] = 0.5*modz; for(i=0;i<N;i++) for(j=0;j<N;j++) Xx[i][j] = fit[i] + dz[i][j]; k = 0; p = Nor(Xx, N); while(p > eps) { k++; Srt(Xx, N); for(i=0;i<N;i++) Xo[i] = 0.; for(i=0;i<N;i++) for(j=0;j<N;j++) Xo[i] += Xx[i][j]; for(i=0;i<N;i++) Xo[i] /= N; for(i=0;i<N;i++) Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]); for(i=0;i<N;i++) fit[i] = Ro[i]; FR = I(); for(i=0;i<N;i++) fit[i] = Xx[i][N]; FN = I(); if(FR > FN) { for(i=0;i<N;i++) for(j=1;j<=N;j++) Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]); } else { for(i=0;i<N;i++) fit[i] = Xx[i][0]; F0 = I(); if(FR < F0) { for(i=0;i<N;i++) Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Eo[i]; FE = I(); if(FE < FR) for(i=0;i<N;i++) Xx[i][N] = Eo[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } else { for(i=0;i<N;i++) fit[i] = Xx[i][N-1]; FNm1 = I(); if(FR <= FNm1) for(i=0;i<N;i++) Xx[i][N] = Ro[i]; else { for(i=0;i<N;i++) Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Co[i]; FC = I(); if(FC < FR) for(i=0;i<N;i++) Xx[i][N] = Co[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } } } for(i=0;i<N;i++) cout << Xx[i][0] << " "; cout << k << " " << p << endl; p = Nor(Xx, N); if(p < eps) break; } for(i=0;i<N;i++) fit[i] = Xx[i][0]; /*for(i=0;i<N;i++) { for(j=0;j<N+1;j++) cout << Xx[i][j] << " "; cout << endl; }*/ delete[]Co; delete[]Xo; delete[]Ro; delete[]Eo; for(i=0;i<N;i++) { delete[]dz[i]; delete[]Xx[i]; } } //возвращает норму вектора D Methods :: Nor(D **X, int N) { int i, j, k; D norm, xij, pn = 0.; for(i=0;i<N;i++) for(j=i+1;j<=N;j++) { xij = 0.; for(k=0;k<N;k++) xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) ); pn = sqrt(xij);//считает длину разности столбцов if(norm > pn) norm = pn;//ищет максимальную длину } return sqrt(norm); } //сортировка координат вершин симплекса void Methods :: Srt(D **X, int N) { int i, j, k; D temp; D *f = new D[N+1]; D *box = new D[N]; D **y = new D*[N+1]; for(i=0;i<N+1;i++)//динамическая память y[i] = new D[N+1]; for(i=0;i<N;i++) box[i] = fit[i];//старые тау в коробку for(i=0;i<=N;i++) { for(j=0;j<N;j++) fit[j] = X[j][i]; f[i] = I();//значения функции в вершинах симплекса } for(i=0;i<N;i++) fit[i] = box[i];//выкладывает тау из коробки for(i=0;i<N;i++) for(j=0;j<=N;j++) y[i][j] = X[i][j]; for(i=0;i<=N;i++) y[N][i] = f[i];//stack(X, f) //Сортирует столбцы матрицы таким образом, //чтобы расположить элементы в строке N в порядке возрастания for(i=1;i<=N;i++) for(j=0;j<=Ni;j++) if(y[N][j] >= y[N][j+1]) for(k=0;k<=N;k++) { temp = y[k][j]; y[k][j] = y[k][j+1]; y[k][j+1] = temp; } //submatrix вырезает отсортированное for(i=0;i<N;i++) for(j=0;j<=N;j++) X[i][j] = y[i][j]; /* for(i=0;i<=N;i++) { for(j=0;j<=N;j++) cout << y[i][j] << " "; cout << endl; } */ for(i=0;i<N+1;i++) delete[]y[i]; delete[]box; delete[]f; } int main() { Methods method; //method.ofDescent(); //method.ofGradient(); method.ofNelder_Mid(); return 0; }

It's enough for today. The next step will be logical to try something from the global optimization, type more test functions, and then examine the packages with built-in methods.



Source: https://habr.com/ru/post/440070/

More articles: